给水管网可靠度的计算

赵新华¹，陈春芳¹,郑毅²?
(1．天津大学 环境工程系，天津 300072；2.天津市自来水集团公司，天津 300040)

　　摘要： 介绍了给水管网可靠度计算的两种方法，重点介绍了最小割集法。首次提出了给水管网计算中管件可用度和平均可用度的概念，并建立了相应的数学模型。通过管网故障状态下水力模拟仿真模块，计算节点和系统的最小割集，利用可用度计算模块，计算出组件的可用度和不可用度，进而求得节点和系统的可靠度。?
　　关键词： 给水管网；最小割集；可靠度；可用度?
　　中图分类号： TU991.33
　　文献标识码： C
　　文章编号： 1000-4602(2000)01-0057-04

　　给水系统的可靠性是指在一定时间内，在一定的运行条件下给水系统完成预定功能的性质。给水系统的功能是保证用水对象获得所需的水量、水压和水质。如果用水过程中发生恶化, 使这三个指标中任意一个下降到允许的限度以下，就说系统发生了故障(本文研究的是水 压 和水量恶化引起故障的情况)。按照系统发生故障的原因，可以将可靠性分成两大类：机械可靠性(Mechanic Reliability)和水力可靠性(Hydraulic Reliability)。前者主要是由于管件发生损坏或被隔断引起的供水能力的下降，通常通过维修或更新来处理；而后者主要是由于长期使用，管件内部摩阻增大，造成水头损失增大而引起,通常可采取水泵调节或 刮管涂衬来处理。本文主要研究基于机械可靠性的给水管网可靠度的计算。

1 可用度模型及可靠度算法

　　对所研究的对象有四点假设：
　　① 部件和系统都只有正常和失效两种状态；
　　② 系统的状态完全由系统的可靠性框图和部件的状态决定；
　　③ 部件的状态转移率,即故障率λ和修复率μ均为常数；
　　④ 组件或系统的故障和修复都是相互独立的。
　　设系统S由n个部件组成，用二值变量X_i来表示第i个部件的状态
　　
　　系统的状态可以用下述函数ø(X)=ø(x₁,x₂,…,x_n)来表示，其中X是n维向量øX=(x₁,x₂,…,x_n)，ø(X)是n维向量的二值函数，即n元二值函数，有
　　
　　把这种n维二值变量的二值函数称为n维结构函数。?
　　计算给水管网可靠度可以采用以下两种方法。
? ① 不交最小路算法
　　a. 对于简单小型管网，可以采用邻接矩阵法求出所有最小路。?
　　b. 对于大型复杂管网，节点数很大，邻接矩阵往往是稀疏矩阵，因此用邻接矩阵法求最小路要大容量去存贮，可以采用计算机算法求最小路。
　　若已知全部最小路集，由初等概率论知
　　
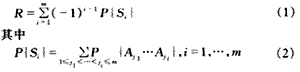
　　但是，当m大时，每个P{S?i}就得由Cmⁱ项概率的和来求得，因此由式(1)求数值结果时共2^m-1项求和(或差)，总的运算量就非常大。因此就要对最小路进行不交化，不交化后可利用相斥事件求和公式：
　　
　　得可靠度：
　　
　　② 对于多水源管网，应用枚举法求系统及节点的最小割集较为方便。
　　本文采用最小割集法(Minimum Cut Set)求节点和系统的可靠度。
　　按图论的理论，所谓割集，就是系统部件的状态变量集合(x₁,x₂,…,x_n)中满 足下列条件的子集：设该子集为{x_j1,…,x_ja},j=1,…,m，{ x_j1,…,x_ja}∈{ x₁,x₂,…,x_n}， 当x_j1=…=x_ja=0时 ,Ø(x)=0，即该子集所对应的全体部件故障时，系统s必定故障。 其中m为割集数，为结构函数。那些去掉一个部件即不构成割集的割集称为最小割集。
　　城市供水管网实际运作是个动态过程，用管网图形的拓扑结构生成最小割集进而计算节点和系统的可靠度，并不能很好地反映供水管网运行状态的实时变化。因此，我们可以采用管网故障状态水力模拟的方法确定实际状态下的最小割集。
　　在实际管网中，当管段发生故障，可以采用关闸方式关闭有关管段进行维修，这时认为管段被从管网中除去, 就可以用水力计算方法进行管段(管段组合)故障状态下的状态模拟。如 果节点水压高程(水量)值小于所要求的节点水压高程(水量)的最低值, 则认为节点发生故障，该管段(管段组合)就是这个节点的一个最小割集，同时也是系统的一个最小割集。对管网中每根管段及管段的组合进行上述模拟，就可以求出节点和系统的全部最小割集。对于一般城市管网，枚举各种管段组合的数量是相当大的，又因为两个以上管段同时发生故障的概率很小，所以可以首先只对单个管段进行故障状态下的模拟，然后对优化结果进行单个管段和两管段同时发生故障的可靠度的计算。如果结果不甚令人满意，可重新考虑对单 个管段和两个管段同时故障时的模拟。
　　在以往的文献中，一般都是以可靠度这个指标来表示给水管网的可靠性。它没有反映出管段、节点和系统的各自特点以及它们之间的相互关系。
　　根据定义，部件寿命分布函数为
? F(t)=P{X≤t},t≥0? (5)
　　记 R(t)=P{X>t}=1-F(t) (6)
　　一般R(t)称为该部件的可靠度函数或可靠度。
　　由定义可知，可靠度表示了部件寿命这个随机变量，对于初始状态部件为完好的情形，F(t) 是部 件首次出现故障前的时间分布，R(t)为从某个初始状态出发，在时刻t仍处于正常状态的概率，这里t是指寿命时间。而给水管网属于可修复系统，对于可修复系统，系统可由正常和故障两个状态不断交替的过程来描述。一般来说，给水系统组件的故障和修复率都服从指数分布。由指数分布的无记忆性可知，初始时刻t以后系统发展的概率规律完全由时刻t是正常还是故障所决定，而与该系统在时刻t已经工作了多长时间或已修理了多长时间无关。因此，组件在任意时刻正常工作的概率应该用可用度A(t)来表示。可用度的定义为：组件在规定的条件下，在任意时刻上正常工作的概率。它的数学式表示为：
　　
　　式中 λ-- 故障强度，也叫失效率，表示单位时间单位长度管线发生故障的次数，a^-1·km^-1 μ-- 修复强度，也叫维修率，表示单位时间管段维修的次数，h^-1这里研究初始时刻部件处于完好状态的情形，同理也可以求得该时刻部件处于故障状态的情形。考虑［0,T］时间段内组件的平均可用度，即为求A(t)的数学期望E［A(t)］。由函数的数学期望公式得：
　　
　　相对于可用度A(t)是不可用度Q(t)，定义为：组件在规定的工作条件下使用时，在任意时刻上处于故障状态的概率。
　　 Q(t) =1-A(t)? (12)
　　研究节点和系统的可靠性，引入可靠度这一概念。节点可靠度的定义为：在某一时间段内，节点的水压高程大于节点所要求的最小水压高程的概率。系统可靠度的定义为：在某一时间段内，所有节点都可靠的概率。
　　设某节点j或系统s的一个最小割集MCi中包含n条管段, 则该最小割集的故障概率为：
　　
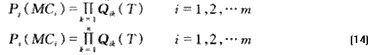
　　设某一节点j或系统s有m个最小割集，则该节点或系统的故障概率为：
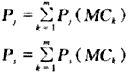　　 　　　　　　　　　　　　　　　　(16)
　　则该节点或系统正常工作的概率为：
　　R_j=1-P_j 　　(17)
　　R_s=1-P_s ? 　(18)
　　本文提出的算法可以用流程图(图1)来表示。

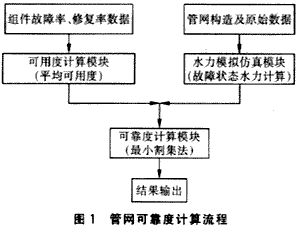
　　其基本步骤是：
　　① 搜集原始数据，获得管网结构图，平差基本数据，组件故障率、修复率资料及节点和系统可靠度指标值。
　　② 用枚举法进行管网故障状态水力模拟，求节点和系统的最小割集。
　　③ 按式(11)、(12)计算组件可用度和不可用度。
　　④ 按式(13)～(18)计算节点和系统的可靠度。?

2 算例

　　本文采用^［1］的管网(图2)对以上提出的算法进行了验算，并编制了相应的程序。

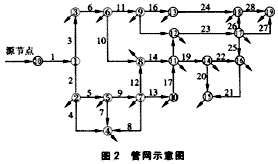
　　对于一些原始数据，如管径、管长、节点流量、节点初始水压、节点压力水头的约束均采用了该篇文章的数据，对于另外一些参数，如故障率、修复率则是通过查阅大量文献资料并结合我国国情现状确定的(见表1)。建议在实际应用中，这些参数从历史资料的统计分析中获得。算例中研究的时间区间为2年，由于该管网规模较小，枚举的运算量不是很大，所以讨论了一条或两条管段故障的情况，在586PⅡ300机上占CPU时间约3min。计算结果见表1。
　　从表1可以看出：水源点附近的点比距离水源点较远的点的可靠性高；当降低故障率或提高修复率时，节点或系统的可靠度都会提高。这一结果对运行的管理和控制有一定的实际指导意义。

3 结论

　　综上所述，讨论给水管网中节点及系统可靠度，首先应在掌握历史资料的基础上，通过统计回归的方法得到各管段的故障及维修参数λ和μ，求出各管段的可用度A(t)和不可用度 Q(t) ，然后调用水力模拟仿真模块计算出各个节点在故障状态下的水压Hj，并与允许的水压最低值H_jmin进行比较，如果H_j＜H_jmin，则模拟的故障管段即为最小割集。在得到各节点及系统的最小割集后，运用可靠度计算模块计算节点及系统的可靠度。

表1 给管网可靠度计算数据及结果 管段号1 起始
节点 终止
节点 管径
(m) 长度
(m) 故障率
(a^-1.km^-1) 修复率
(h^-1) 节点
编号 节点流量
(L/s) 水压高程约束
(m) 可靠度 1 20 1 0.50 450 0.0140 0.50 1 0 710 0.9898 2 1 2 0.43 70 0.0165 0.50 2 2 710 0.9778 3 1 3 0.33 545 0.0230 0.50 3 10 710 0.9759 4 2 4 0.23 463 0.0375 0.50 4 14 710 0.9759 5 2 5 0.43 160 0.0375 0.50 5 5 710 0.9657 6 3 6 0.33 263 0.0165 0.50 6 2 710 0.9632 7 5 4 0.15 435 0.0230 0.50 7 15 710 0.9530 8 7 8 0.10 1115 0.0490 0.50 8 8 710 0.9526 9 5 7 0.40 180 0.0510 0.50 9 2 710 0.9521 10 6 8 0.45 495 0.0175 0.50 10 4 710 0.9524 11 6 9 0.40 180 0.0175 0.50 11 8 710 0.9521 12 7 8 0.35 170 0.0210 0.50 12 10 710 0.9499 13 7 10 0.40 270 0.0175 0.50 13 2 710 0.9501 14 8 11 0.30 396 0.0250 0.50 14 2 710 0.9495 15 9 12 0.20 555 0.0445 0.50 15 8 710 0.9445 16 9 13 0.25 123 0.0285 0.50 16 9 710 0.9460 17 10 11 0.40 305 0.0175 0.50 17 12 710 0.9461 18 11 12 0.38 72 0.0190 0.50 18 11 710 0.9461 19 11 14 0.20 180 0.0445 0.50 19 7 710 0.9081 20 14 15 0.15 600 0.0490 0.50 20 -131 710 1.0000 21 16 15 0.20 130 0.0445 0.50 　 　 　 　 22 14 16 0.18 430 0.0460 0.50 　 　 　 　 23 12 17 0.40 225 0.0175 0.50 　 　 　 　 24 13 18 0.20 450 0.445 0.50 　 　 　 　 25 17 16 0.25 235 0.0285 0.50 　 　 　 　 26 17 18 0.20 352 0.0445 0.50 　 　 　 　 27 17 19 0.15 590 0.0490 0.50 　 　 　 　 28 18 19 0.10 645 0.0510 0.50 　 　 　 　

参考文献：
［1］ 徐祖信.水分配系统以可靠性为基础的线性优化模式［J］.同济大学学报, 1996，5.
［2］ 布拉莫夫.给水系统可靠性［M］.北京：中国建筑工业出版社，1990.

---

电话： (022)27400830(O)