均质滤料滤床过滤数学模型
| 论文类型 | 技术与工程 | 发表日期 | 2000-11-01 |
| 来源 | 第四届全国给水排水青年学术年会 | ||
| 作者 | 景有海,金同轨,范瑾初 | ||
| 摘要 | 景有海 金同轨 范瑾初 西安建筑科技大学 同济大学 1、 均质滤料滤床的毛细管模型 由粒状材料组成的均质滤料滤床,内部有无数孔隙通道。水流通过滤层的过滤过程,就是水流在滤床孔隙内的流动时,滤料表面对水中悬浮颗粒的吸附过程。在目前常规滤速范围内,滤层孔隙内水流的流态为层流,其流 ... | ||
景有海 金同轨 范瑾初
西安建筑科技大学 同济大学
1、 均质滤料滤床的毛细管模型
由粒状材料组成的均质滤料滤床,内部有无数孔隙通道。水流通过滤层的过滤过程,就是水流在滤床孔隙内的流动时,滤料表面对水中悬浮颗粒的吸附过程。在目前常规滤速范围内,滤层孔隙内水流的流态为层流,其流线既不会交叉,也不会消失,当然也不会重生。由于滤料的阻挡,水流只能出现部分的分与合,而总的流动趋势是垂直向下的。因此,可将这样的滤床看成是有无数条毛细管道组成的管束网,过滤过程可看作是水流在这些毛细管道中流动时,毛细管壁对水中悬浮颗粒的吸附过程。为了使水流在毛细管道中的过滤条件与实际滤床中的过滤条件相同,毛细管必须满足以下两个条件:
(1)毛细管道的空间应与滤床的孔隙相同;
(2)毛细管道的总表面积应与滤池中滤料的总表面积相同。
因此,如下两个方程应成立:
ε=n.(π/4)d2m
f=n.πdm
式中:ε——滤床的孔隙率(m3/m3);
f——滤料的比表面积(m2/m3);
dm——毛细管的管径(m);
n——单位面积滤池所拥有的毛细管数量(根/m2)
级配滤料的比表面积可表示为:
f=6a(1-ε)/de
式中:a——滤料的表面形状系数,指滤料的表面积与同体积球体面积的比值;
de ——滤料的当量直径(m);
其他符号同前。
联解(1)、(2)和(3)式可得:
dm=[2ε/3a(1-ε)]de
n=9a2(1-ε)2/(πεd2e)
(4)和(5)式即为笔者将均质滤料池抽象为毛细管模型时的毛细管管径和单位面积滤池拥有的毛细管数量的计算公式。
2、过滤过程中的浊质去除计算模型
2.1悬浮物去除机理
研究证明,过滤是依靠滤料表面的吸附性来去除水中悬浮颗粒的。由于滤层中的水流处于层流状态,因此不会有涡旋产生,流线不会出现交叉、新生或消失。处于滤料表面附近流线上的县浮颗粒,当其与滤料表面极为接近时,会被滤料表面吸附截留,其颗粒物浓度随之下降。此时,与处于中心附近流线上的悬浮颗料间出现浓度梯度。在存在尝试梯度的条件下,由分子扩散作用以及由水流速度梯度所引起的水力扩散作用下,使得处于中心附近流线上的悬浮颗粒向滤料表面迁移,最后被滤料表面截留而去除。因此,悬浮颗粒物的浓度梯度是颗粒向滤料表面迁移的主要推动力。
悬浮颗粒运运到滤料表面附近后,会受到颗粒间的吸引力和电场斥力的共同作用。当颗粒间的吸引力大于电场斥力时,悬浮颗粒将被滤粒吸附截留而得以去除。
另一方面,由于水流速度梯度的存在,必将在固体边界处产生剪切力,水流对吸附在滤料表面上的悬浮颗粒与滤料表面间的吸附力(粘着力)大于水流的剪切力时,悬浮颗粒才可继续保留在滤料表面上,否则,将会被水流剪切力剥落下来,再次回到水中。剪切力的大小由滤层孔隙中水流速度梯度决定,而悬浮颗粒与滤料表面的粘着力以及悬浮颗粒与颗粒之间的粘着力则由悬浮颗粒的混凝特性决定。
对于滤池,可看作是由无数颗滤料组成的一个有限流场,每一颗滤料对水流中的悬浮颗粒都具有吸附截留作用,在每一颗滤料表面附近都存在边界层。这样,在滤料表面上,吸附与剥离作用将同时存在。随着过滤过程的进行,滤池截留的悬浮物增多,滤料孔隙率减小,水流速度增大,阻力加大,剪切力也随之加大,从而造成剥离速度加快,总的去除率减缓,并趋向于零。
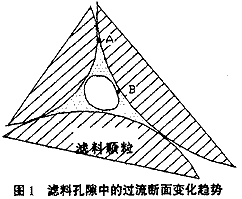
滤床截留浊质后,其孔隙率减小,滤料对水中浊质的吸附面积也将相应减小,这可由图1加以说明。对水而言,当固体边界固定时,水将充满整个固体边界。但由于水具有粘性,其在固体边界处的流速为0,而在过流断面几何中心处,其流速最大。因滤层中水流处于层流状态,因此,在距离过流断面几何中心较远的A点方向上,其流速梯度小于距离过流断面几何中心较近的B点方向上的流速梯度,水流对A点的冲刷力将小于对B点的冲刷力。当因体边界具有随意可变性时,由于水表面张力的作用,它有使其与固体的交界面(湿周)达到最小的趋势,从而使其表面能降低。而圆则具有过流面积最大,其边界最小的特性。因此,A点将首先被浊质填充,使其固体边界逐渐变小,并趋于圆形断面。所以说,当滤床截留浊质后,在其孔隙率减小的同时,滤料的吸附表面积也将相应的减小,而不会增大。
2.2 过滤方程
当把滤池的过滤过程描述为毛细管管壁对水中悬浮颗粒的吸附过程时,可利用毛细管模型来推求过滤过程中的浊质去除计算模型。
2.2.1滤层堵塞方程
在滤层中取某一毛细管作为考查对象,在深度Z处取断面1,并在深度Z+dz处取断面2,如图2所示。设在过滤时刻。设在过滤时刻t,断面1处的浊质浓度为c,则断面2处的浊质浓度为:

水中浊质被毛细管管壁吸附后,其管壁附近的浊质浓度下降,使得毛细管中心附近浊质与管壁附近出现浓度梯度。在浓度梯度的推动下,管中心浊质将向管壁扩散。这种扩散包括布朗运动扩散和水力推散。其扩散速度可表示为:
![]()
式中:υ——浊质的扩散速度(m3/m2.S)
D——浊质的扩散系数(m2/S)
rm——毛细管吸附浊质后的孔道半径(m)
假设浊质一旦扩散到毛细管管壁,即认为被管壁截留,这同理想沉淀池的原理是相同的。因此,经过dt时段后,其扩散量也就是沉积量为:
dGk=υkπdmdzdt≈D(c/rm)πdmdzdt=2πDcdzdt (7)
式中:dGk——浊质的沉积量(m3)
dm——毛细管吸附浊质后的孔道直径(m)。
沉积在毛细管壁上的浊质,会因水流的剪切力而被剥落下来再次回到水中,设其剥离速率与水流的剪切力和毛细管道的堵塞率成正比。若令沉积在单根毛细管管壁单位长度上的浊质体积量为σd(m3/m.根),则有:
σd=σ/n (8)
式中:σ——比沉积量(m3/m3),指单位体积滤层中沉积的浊质体积量。
因此,浊质的剥离速率可表示为:
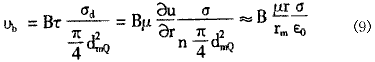
式中:υb——浊质的剥离速率(m3/m2.s)
B——浊质的剥离系数(m3/N.s),它与滤料的表面特性以及水中浊质颗粒的表面特性即混凝特性有关。混凝效果好,则B值小,否则B值大
u——孔道中的水流速度(m/s);
τ——水流的剪切应力(N/m2);
μ——水的动力粘性系数(Pa.s);
dmQ——毛细管原始直径(m);
ε0—清洁滤层的孔隙率。
则经过dt时段后的浊质剥离量为:
![]()
式中:dGb——浊质的剥离量(m3)。
经过dt时段后,毛细管dz管长上截留的浊质量可表示为:
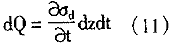
式中:dQ——毛细管上截留的浊质量(m3)。
根据物质不灭定律有:

称λ1为截留系数,λ2为剥离系数,通称为过滤系数。
又因为u=(υ/ε)=υ/(ε0-σ),其中υ为滤速(空塔速度),则(14)式可改写为:
![]()
(17)式描述了滤层的堵塞过程,可称其为滤层的堵塞方程。该式即为本文作者利用毛细管模型推导出的均质滤料滤床过程的滤层堵塞方程式。
2.2.2 连续性方程
在dt时段内,由水流输送净流入dz长度毛细管单元中的浊质量为:

(22)式描述了滤层中截留的浊质与水流中残存悬浮物的相互关系,可称其为过滤过程中的连续性方程。
上式中c为过滤流体中的浊质体积浓度,其单位为(m3固体/m3液体)。显然,c的最大值为I。当c=1时,表示过滤介质已变成固体。在一般的流体过滤过程中,其浊质浓度c<<1,则(22)式可简化为:
![]()
式(22)和(23)即为本文作者推导出的均质滤料过滤过程中的连续性方程。
2.2.3 过滤方程
由连续性方程(22)式可得:
![]()
将(17)式代入(24)式得:
![]()
同理,在一般的过滤过程中有c<<1,则(25)式可简化为:
![]()
式(25)和(26)描述了水中悬浮物质的去除过程,可称其为浊质去除方程或过滤方程。
该两式也是笔者首次利用毛细管模型推导出的均质滤料滤床的过滤方程。
由(17)式和(26)式可以看出:当比沉积量σ≠而进水浊质浓度c=0,悬浮物的去除速率为正值,而滤层中比沉积量的沉积速率为负值.这说明由于水流对沉积在滤料表面上的浊质的剥离,使得水中浊质浓度在增加,而比沉积量在减小。方程描述的这一物理意义与实际过滤过程中的物理现象是相符的,它正好描述了正向冲洗时的滤层清洁过程。因此可以说,(17)、(23)和(26)式不但是过滤方程,同时也是滤层在不扰动情况下的反冲洗方程,这正好说明反冲洗过程是过滤过程的逆过程。
3 过滤方程式的简化分析
3.1 滤层中的最大比沉积量
当滤层吸附饱和而失去除浊能力时,其比沉积量的变化速率为0,因此可令滤层堵塞方程式(17)式中的![]() 即可求得滤层的最大饱和吸附量σmax。此时进入该层的悬浮物浓度应等于原水浓度,即c=c0,因此有:
即可求得滤层的最大饱和吸附量σmax。此时进入该层的悬浮物浓度应等于原水浓度,即c=c0,因此有:
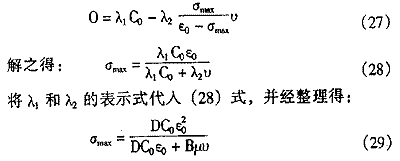
由(29)式可以得出如下结论:
(1)当过滤流体为无粘性的理想流体时,有μ=0。则:σmax=ε0;
(2)当悬浮颗粒与滤料表面的粘附力无究大时,则滤层将无浊质剥落,此时有B=0。则有:σmax=ε0;
这说明在这两种极端情况下,滤层所能截留的浊质量最多为它的孔隙率。
(3)提高滤速,则最大比沉积量减小;
(4)进水浓度提高,则最大比沉积量增大;
将(29)式两边同除清洁滤层孔隙率ε0,则得滤层的最大堵塞率ξmax为;
ξmax=σmax/ε0=DC0ε0/(Dε0+Bμν) (30)
3.2 滤层开始饱和时所需要的过滤时间
在滤池表层,有z=0,c=c0=常数。因此,滤层堵塞方程(17)可写为:
![]()
式中:σi——滤池表层(z=0)的比沉积量。
当过滤是从清洁滤层开始进行时,有当t=0时,σi=0。
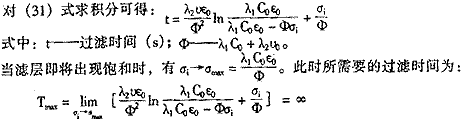
上式表明,在有限的过滤时间内,从理论意义上来讲,滤层中不可能有所谓的“饱和”阶段出现。这是因为:过滤也是一种吸附过程,随着过滤的不断进行,其吸附推动力逐渐减弱,吸附速率(去除速率)逐渐减缓,但不可能完全停止。这一原理与其他多种物理过程,包括化学反应过程一样,是一个无限趋近的过程。因此,理论上滤层是难以达到完全饱和。
在实际应用中,可取当σ=95%σmax时,即可认为滤层已达到饱和状态。此时所需要的过滤时间为:
![]()
3.3 比沉积量沿滤层深度方向上的分布规律
在滤层中取某一毛细管作为考查对象,如图3所示。由表层算起考场 细管长度为z,进入毛细管的浊质浓度为C。经过时间t过滤后,毛细管单位长度上的浊质沉积量为σd,根据物粒平衡关系有:
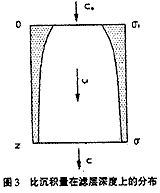
上式等号左侧第2项表示滤层孔隙中残存的悬浮颗粒物量。当过滤时间较长时,该项与其他项相比,可忽略不计。因此(35)式可进一步简化为:
![]()
由方程(17)得
![]()

因udt=dz,而在z断在处有当t=0时,z=z,当t=t时,z=z’,其中z’为假设毛细管无限长时,经过t时间段后,流体沿毛细管流行的距离,因此有:

(43)式即为比沉积量沿滤层深度方向上的分布规律。将(43)和(17)两式合并可得:
![]()
由于(43)式中σ与函数c有关,因此求解较为困难。现对简化式(44)求积分得:
σ=σ1e-[(λ1/ν)-λ2]z (46)
此即为比沉积量沿滤层深度上的近似分布。该式表示:在过滤过程中,滤层中的比沉积量沿深度方向近似按负指数规律衰减。提高滤速,则比沉积量衰减率减小,浊质向滤层深处穿透,比沉积量在滤层中的分布趋于均匀。混凝效果提高,λ2减小,比沉积量衰减率增大,表明浊质较易被表层截留。由于σi与过滤时间有关,因此,σ也是过滤时间t的函数。
将λ1和λ2的值代入上式得:
σ=σ1e(8/d2mo)[(Dε0/ν)Bμ]z (47)
3.4 水中浊质浓度在滤层深度方向上的变化
在常规过滤过程中,滤层中的比沉积量σ远小于滤层的孔隙率,特别是在滤层深入更是如此,则过滤方程(36)可简化为:
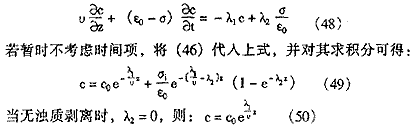
(49)式说明,由于水流剥离力的存在,水中浊质浓度比理想情况增加了一项,使出水浓度有所增加。
因在求解时忽略了ε0-σ中的σ,因此将(49)式进行适当修正得:
![]()
此式即水中浊质在滤层深度方向上的分布。上式说明,浊质沉滤层也近似符合负指数规律。将滤层深度L代入上式即可求得滤池出水浓度。
4 过滤水头损失
4.1清洁滤层的水头损失
当将均质滤料床抽象为毛细管模型时,可利用水流在毛细管中流动时的水头损失计算水流通过层的水头损失 。
水流在均匀圆管内流动时的水头损失可按下式计算:
hf=λ(lu2/d2g) (52)
式中:hf——摩阻水头损失(mH2O);
λ——摩阻系数;
l——管道长度(m);
d——管径(m);
u——管内平均流速(m/s);
g——策略加速度(m/s2);
当水流状态为层流时,其摩阻系数λ只与雷诺数Re有关,即:
λ=f(Re)=64/Re (53)
式中:Re——圆管内水流雷诺数,其定义为:
Re=ρud/μ (54)
式中:ρ——水的密度(kg/m3);
μ——水的动力粘性系数(Pa.s)。
由于在滤池的毛细管模型中,毛细管为抽象的管道,而非实际圆管,因此,其阻力系数不能直接套用(53)式,但可仿效它。令抽象毛细管的摩阻系数为
λ=C/Re (55)
根据敏茨对粒状材料过滤的大量统计学资料,可求得:C=163.2(其推求过程这里从略)。
将(52)式和(55)式应用到滤池的毛细管模型中,即可求得水流通过滤层的水头损失。
水流通过△L厚度滤层,相当于水流沿毛细管流过△L长度,其水头损失为:

此式即为水流通过滤层时的水头损失计算公式。
对于均质滤料清洁滤层,其滤料的表面形状系数a、当量直径de和滤层的孔隙率ε均为常数,因此,均质滤料清洁滤层的水头损失可表示为:
![]()
式中:H0——清洁滤层的水头损失(mH2O);
a0——清洁滤料的表面形状系数;
ε0——清洁滤层的孔隙率;
de0——清洁滤料的当量直径(m)。
4.2 堵塞滤层的水头损失
当滤池经过一段时间过滤后,滤层受到截留悬浮物的堵塞,使其孔隙率减小,这相当于毛细管的管径缩小。设毛细管单位管长截留的悬浮物量为σd,毛细管管径由dm0缩小至dm,则下式等式成立:
(π/4)d2m0-(π/4)d2m=σd (59)
因此有:
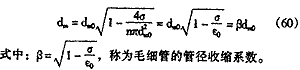
对于恒速过滤,其过滤流量不变,当毛细管径缩小后,其孔道内流速必将增大。根据流体的连续性方程可得:
(π/4)d2m0.u0=(π/4)d2m.u
式中:u0——清洁管道中的流速(m/s);
u——毛细管截留浊质后的孔道流速(m/s);
即 u=u0[dm0/dm]2=u0/β2 (61)
此时的雷诺数为:
![]()
式中:Re0——清洁孔道中的雷诺数。
因此,滤层截留留悬浮物后,其△L厚度滤层的水头损失为:

将滤层中的比沉积量分布函数(46)式代入上式,求积分并经整理可得:
Ht=Kt.H0 (65)
式中:Ht——堵塞滤层的水头损失(mH2O);
H0——清洁滤层的水头损失(mH2O);
Kt——水头损失增长系数,其值为:
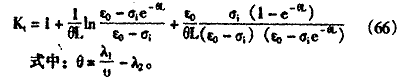
式是:θ=(λ1/ν)-λ2
L——滤层厚度(m)。
式(65)说明,过滤过程中的水头损失等于清洁滤层的水头损失乘以滤层因被截留浊质堵塞而使水头损失增长的系数。因水头损失增长系数Kt与表层比沉积量有关,因此堵塞滤层的水头损失也是过滤时间的函数。
5 过滤特性与滤料粒径和滤层厚度的关系
滤池的过滤特性可以用它的水头损失和滤出水浊度两个特性来表征
5.1 过滤水头损失
由(58)式可知,清洁滤层的水头损失与滤层厚度成正比,而与滤料的当量走私的平方成反比。即在其他条件不变的情况下,清洁滤层的水头损失可表示为如下函数形式:
H0=f0[L0/d2e0] (67)
由(65)式可知,过滤过程中的水头损失等于清洁滤层水头损失乘于水头损失增长系数Kt,而Kt与(λ1/ν)L0和λ2L0有关,但:
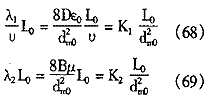
由(4)式可知,dmo∝de0,因此,水头损失增长系数Kt可表示为:
![]()
则过滤过程中的水头损失Ht可表示成如下函数形式:
![]()
由此可知,无论是清洁滤层还是过滤过程中,其水头损失与滤池的L0/d2e0相关。
5.2 滤池出水浊度
由(51)时可,滤池的出水浊度也是与(λ1/ν)L0和λ2L0有关,因此,其出水浊度可表示成如下函数形式;
c=fc[L0/d2e0,t] (72)
也就是说,滤池的出水浊度与滤池的L0/d2e0相关。
综合以上两方面的分析可以得出结论:滤池的过滤特性与滤层深度和滤料当量直径平方的比值相关,即与滤池的L0/d2e0相关。只有当滤池的L0/d2e0相同时,其过滤特性才可相同或相当。
虽然增大滤料径可减小水头损失,但随之带来的是出水水质的恶化或过滤周期的缩短。因此可以说,依靠增大滤料粒径的方法来减少过滤中能量消耗的这一途径是行不通的,也是不符合能量守恒原理的。因此要想将悬浮颗粒从水中去除,必须付出一定的代价,也就是能量消耗。
6 结论
(1)将滤池抽象为毛细管模型后,可简化过滤过程的数学描述。毛细管管径和单位滤池面积上的毛细管管束数与滤料的当量直径、孔隙率和表面形状系数有关;
(2)由于水本身具有的特性,当滤层截留悬浮物后,在其孔隙率减小的同时,滤料的吸附表面积也在相应的减小,不会增大;
(3)均质滤料过滤过程中,滤层中的比沉积量在滤层深度上近似呈负指数规律变化,浊质浓度也近似符合负指数规律;
(4)在有限的过滤时间内,理论上滤层难以彻底失去除浊能力,因此也就不可能出现所谓的“安全饱和”阶段;
(5)滤层中的最大比沉积量不但与进水悬浮物浓度有关,而且还与滤速有关;
(6)过滤过程中滤层水头损失等于清洁滤层的水头损失乘以滤层因被浊质堵塞而使水头损失增加的系数。
(7)滤池的过滤特性与滤层深度和滤料当量直径平方的比值相关,只有当滤池的L0/d2e0相同时,其过滤特性才可相同或相当。
参考文献
[1] 许保玖、安鼎年,《给水处理理论与设计》,中国建筑工业出版社,1992年11月;
[2]严熙世、范瑾初,《给水工程》,中国建筑工业出版社,1995年6月;
[3][苏]ю.M.康士坦丁诺夫著,钟用升译,《水力学》,江西高校出版社,1990年7月;
[4][苏]д.м.明茨,C.A.舒别尔特著,惠遇甲译,《粒状材料水力学》,水力出版社,1955年;
论文搜索
月热点论文
论文投稿
很多时候您的文章总是无缘变成铅字。研究做到关键时,试验有了起色时,是不是想和同行探讨一下,工作中有了心得,您是不是很想与人分享,那么不要只是默默工作了,写下来吧!投稿时,请以附件形式发至 paper@h2o-china.com ,请注明论文投稿。一旦采用,我们会为您增加100枚金币。








