冷却塔设计的计算机运算程序

胡连江¹，孙慧²,蔡广³
(1.天津石化设计院，天津 300271；2.上海深圳物业发展有限公司，上海 201108；3.西北建筑工程学院，陕西 西安 710061)

　　摘要：开发的冷却塔计算机运算程序，可以把专业人员从繁琐的人工计算中解脱出来，同时运算精度也得以大幅度提高，同时介绍了计算方法的选择优化和程序编制以及变量确定的一些技巧。
　　关键词：冷却塔； 设计； 运算程序
　　中图分类号：TU991.42
　　文献标识码：C
　　文章编号：1000-4602(2000)12-0039-04

　　水的循环使用是节约用水的重要途径，冷却塔又是水循环使用的关键设备，从某种意义上讲，冷却塔技术是循环水技术的核心。冷却塔的设计计算一直是专业人员比较棘手的工作，这是因为繁杂的人工运算是很困难的，而采用简化算法精度又不够。因此，冷却塔计算机运算
程序的开发成功，为新型冷却塔的研制和开发提供了条件。

　　1 冷却塔的设计计算

　　冷却塔的设计计算主要包括热力计算和空气动力计算两个方面，程序运算框图见图1。

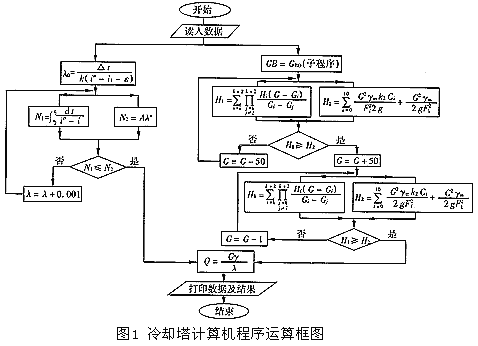
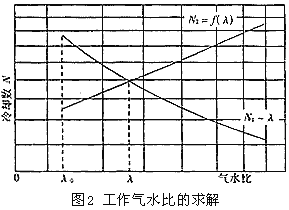
　　热力计算目前广泛采用的是麦克尔（Merkel）1925年提出的热焓平衡及焓差方程，该方程从冷却的角度描述了水传热和湿空气吸热过程的热力特性，并由此演变出冷却数N的方程［式(1)］，它与J·李钦斯特(Lichtenstien)1943年从填料试验中归纳出的填料散热特性方程［式(2)］联立求解，即可求得工作气水比(见图2)。

　　
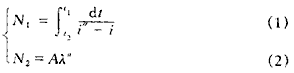
　　式中　 N ——冷却数
　　　　　t₁——进塔温度
　　　　　t₂——出塔温度
　　　　　A——常数
　　　　　λ——气水比
　　　　　i″——空气饱和焓
　　　　　i——空气焓
　　　　　n——常数
　　空气动力学计算是通过对风机的特性方程［式(3)］和冷却塔的阻力特性方程［式(4)］联立求解，求得工作风量。风机的特性方程需由风机特性曲线拟合得来。

　　

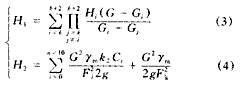
　　 式中　H₁ ——风机全压
　　　　　H₂——冷却塔阻力与全压之和
　　　　　γ_m——空气的平均体积质量
　　　　　k₂——阻力系数
　　　　　C_i——冷却塔内各部位的阻力
　　　　　F_i——冷却塔内各部位的通风面积
　　　　　F_k——风筒扩散筒上口的通风面积
　　　　　G——风量

　　2 计算方法的优化

　　2.1 冷却数N
　　冷却数N的表达式为积分式，对于积分的求解方法很多，其中经典的为辛普逊(Simpson)积分法。手算时一般采用简化辛普逊法(辛氏三分之一法)，此方法是以Δt/2为分割点，将曲线分成两段，近似求解，但当Δt＞15 ℃时计算误差就会很大，简化算法都难以满足。为提高计算精度，在程序编制时应采用复化辛普逊法，数学原型为：。简化辛普逊法只相当于复化辛普逊法m＝1时的精度，当m＝1000时，曲线将被分割为2000段，此时精度已达到千亿分之一(辛普逊积分法的最大误差值为（Δt／180n^4｜Δi｜)，计算机完成这些运算仅需3～4s，用这个结果去校验手算值(上海科学技术出版社1981年的出版《冷却塔》一书中的例题)，均有3.9%～7.79%的误差(见表1)。分析误差产生的原因有三：一为公式因素，手算时n不可能取很大，一般取2，即简化辛普逊法；二为取舍误差；三为查表误差。

表1 手算与电算结果对照表 参




数 气水比λ 0.5 0.6 0.9 进塔温度t1(℃) 40.24 40.24 40.24 出塔温度t2(℃) 32 32 32 干球温度θ(℃) 25.7 25.7 25.7 湿球温度τ(℃) 22.8 22.8 22.8 大气压力(kPa) 99.658 99.658 99.658 结

果 手算冷却数N 1.024 0.861 0.692 电算冷却数N 0.95 0.807 0.666 差值(%) 7.79 6.69 3.9

　　 2.2 风机特性方程
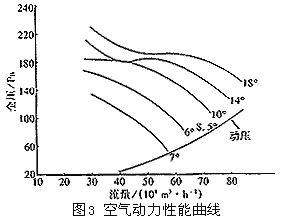
　　一般风机厂不提供风机特性方程，仅提供风机特性曲线，计算时需对风机特性曲线进行拟合。风机特性曲线拟合的方法很多，一般广为采用的是二次抛物线法，其函数表达式为：H=ax2-bx-c(H为风机全压，x为风量，a、b、c为常数)，此方法直观、简便，在特定区间具有一定的精度，但缺点是局限性太大，因二次抛物线法函数的一阶导数为H′=2ax-b，系单调函数，而风机特性曲线并非都具有一阶导数单调性的特性，以4.7 m风机特性曲线为例(见图3)，当叶片角度≥14°时，曲线的一阶导数不单调，曲线多次出现震荡，特别是对风机原始参数分析结果表明，此种现象是经常的、大量的，因此用二次抛物线法描述风机特性是不理想的。
　　笔者在程序编制中采用了拉格朗日(Lagrange)一元三点插值法对风机特性曲线进行数值逼近，有效地避免了二次抛物线法的上述缺点，此法为分段二次抛物插值法，逼近效果优于经典拉格朗日插值法，且可避免经典拉格朗日插值法在高次插值时出现的龙格(Runge)现象。用风机厂提供的原始数据验算此法，均方差为0.008%。其数学原型为：。

　　3 气水比的计算

　　3.1 工作气水比λ
　　工作气水比λ系通过求解方程式(1)和(2)的联立方程组求得工作气水比。鉴于方程组为非线性方程组，直接求解很困难，程序运算一般采用试算法，先假定一个较小的气水比λ0，代入式(1)求得N₁值，代入式(2)求得另一个N₂值。由图2可见，当气水比由小向大逼近时，联立方程组有如下特性：在曲线的交点左侧，N₁＞N₂，随着气水比的增加，差值越来越小，直至N₁=N₂，即两条曲线的交点就是联立方程组的解，此时气水比即工作气水比。根据这一特性，循环终止条件可设置为N₁≤N₂，否则气水比再加上一个微小值(步长)，即λ=λ+Δ，重新代入式(1)、(2)计算，重新比较，直至求解。
　　3.2 初始气水比λ0的确定
　　前述已知，气水比是从一个较小的值向大值逐步逼近循环试算的，因此初始气水比λ0就要足够小，否则就有可能使方程越过两条曲线的交点，致使联立方程组无解，在程序运算过程中将形成死循环。然而从0开始又会增加很多无谓的运算，不必要。那么怎样确定为最佳呢?分析出塔空气焓的函数关系式：i₂=i₁+Δt/kλ，可知当λ变小时，i₂就会增大，λ小到一定值时，i₂将会增大到比进塔水温t₁所对应饱和空气焓i″1还大，也就意味着此时空气非但不能冷却水，相反还要向水中散热，这是与冷却塔任务相反的工况，超出了冷却塔焓差的定义域，也就是说i₂大到极限趋近于i″1。因此可以假定i₂=i″1-ε(ε为足够小)，此时的气水比是趋近于最小极限的气水比(具有实际意义值)，即λ₀=Δt/[k(i″₁-i₁-ε)。

　　4 风量的计算

　　4.1 工作风量的计算
　　冷却塔风机工作风量的计算是计算风机在冷却塔特定环境——特定的阻力、动压、空气密度及水量的条件下可提供的风量，同时确定工作风压及此时的风机轴功率。风机工作风量是通过式(3)、(4)的联立方程组求得。式(3)是风机全压与风量的函数关系式，通过一元三点插值法对风机特性曲线拟合得来，对于该方程式直接求解目前还很困难，因此仍采用试算法。
　　鉴于从4.7 m到9.14 m风机的风量变化范围较大(60×10⁴～300×10⁴m³/h)，循环过程中较大的步长精度难以保证，小的步长对于大风机的风量计算来说，循环量又太大，因此宜将循环分成两个阶段，在第一阶段采用大步长(Δ=50m³/h)以减少运算次数。假定风量由大向小逼近，联立方程组在两条曲线的交点右侧应有H₁＜H₂，随着风量减少，差值越来越小，直至H₁=H₂，即两条曲线的交点，也就是联立方程组的解，此时的风量即工作风量。因此当H₁≥H₂时，两条曲线已处于交点或越过交点，此时进入第二阶段循环。为使程序循环进行下去，在第二阶段循环的开始，应在第一阶段循环的基础上退回一步，即第一阶段里每循环一步，风量将减去一个步长(Δ=50m³/h)，完成第一阶段的循环，此时的风量将作为第二阶段循环的初始风量，但应先补回一个50m³/h，然后开始第二阶段循环。第二阶段采用小步长(Δ=1m³/h)，这样设置之后不仅提高了运算速度，而且计算精度也可控制在0.01%以下。
　　4.2 初始风量的设定
　　一元三点插值法对选取点的要求是必须在插值点所在的区间，即区间［最小插值点，最大插值点］，否则函数会发生质的改变，也因此在确定初始风量时首先要满足这个要求。由式(4)可知，塔内阻力与风量的平方成正比，程序可利用这一特性，先假定一个偏小的风量，代入式(4)后算出H(塔内的总阻力与动压之和)，持此值与风机全压的最大插值点比较，若小于最大插值点，则风量加100m³/h，再代入式(4)循环试算，直至大于或等于风机全压的最大插值点时，将此时的风量再减去100作为初始风量。

　　5 结语

　　冷却塔计算程序的编制，使得繁锁的冷却塔计算变得轻而易举，手算需要几个工日的工作现在只需几秒钟，而且大大地提高了计算精度，这不仅为冷却塔的计算提供了方便，也为新型冷却塔的研制和开发奠定了基础。几年来，采用此程序对很多工程进行了计算，经测试表明，计算准确，结果可信。在此基础上，并结合多年冷却塔工程设计经验，终于研制出“全流道流线型冷却塔”(已获得专利，专利号为：ZL 95 1 04965.8)。

　　参考文献：
　　［1］李德兴.冷却塔［M］.上海：上海科学技术出版社,1981.
　　［2］赵振国.冷却塔［M］.北京：水利电力出版社,1997.
　　［3］电子计算机算法手册［M］.上海：上海教育出版社,1982.

---

电话：(022)63804253
传真：(022)25990266
E-mail:tpdinet@public.tpt.tj.cn
收稿日期：2000-06-08