悬浊液透光脉动颗粒在线检测技术及其应用（一）

于水利，李圭白，田永平
（哈尔滨工业大学市政与环境工程学院，黑龙江 哈尔滨150090）

　　摘　要：在国外现有研究的基础上，从理论上推导出了悬浊液透光率脉动值的解析式。对该解析式的进一步研究表明，悬浊液透光率脉动值V_R或R（R＝V_R/V）主要与悬浊颗粒大小有关，颗粒个数浓度N对V_R或R的影响较小，悬浊颗粒凝聚时透光率脉动值总是增大的。给出了单一粒径组成和具有一定粒径分布的悬浊液，根据其透光率脉动值计算颗粒平均粒径的解析式。
　　关键词：悬浊液；透光脉动；悬浊颗粒；检测；传感器
　　中图分类号：X832
　　文献标识码：A
　　文章编号：1009－2455（2001）01－0001－05

An On-Line Monitoring Technique for Transmitted Light Fluctuation
in High-Turbidity Water and Its Application
——A Theory of Monitoring for Transmitted Light Fluctuating Particles
YU Shui-li，LI Gui-bai，TIAN Yong-ping
(Sch.of Municipal & Environ. Engin.，Harbin Insistute of Technology，Harbin 150090，china)

　　Abstract:Based on the present research abroved, an analytical formula for transmitted light fluctuation (TLF) value of suspension liquid id deduced theoretical.Further research into this analytical formula shows that the TLF value of V_R or R(R=V_R/V) of suspension liquid is primarily related to the sizes of suspended particles while the concentration of the number of the particles has less influence on V_R or R, and that TLF value always increases when suspended particles coagulate. An analytical formula is given to calcuate the average value of the size of the particles of a given suspension liquid having single particles size on the basis of its TLF value.
　　Key words:suspension liquid；transmitted light fluctuation；suspended particle；monitoring；transducer

前言

　　悬浊颗粒的检测，目前国内外常用以光学检测为基础的各种光散射计数器，如：Coulter颗粒分析仪^[1]及Hiac计数器^[2]等。这些方法存在受光照射水样体积小，检测的只是单个粒子的行为，并需对检测结果进行脉冲高度分析，不能实现在线连续检测，
测定时需要对水样进行稀释，以避免颗粒的重叠，以及絮凝体在通过Coulter孔口或Hiac计数器的检测区时被打碎，测定费时费力等问题。20世纪80年代后期，Gregory和Nelson^[3]首次发现悬浊液透光率脉动值与悬浊颗粒粒径有关，并就该相关关系进行解
析，从而为悬浊颗粒粒径检测传感器研究开辟了新的途径。
　　本文在国外透光脉动研究的基础上，进一步对透光脉动理论进行探讨，从理论上搞清了透光脉动值与悬浊颗粒的粒径、分布及浓度的关系。

1 透光脉动悬浊颗粒检测理论

　　1.1 悬浊液浊度
　　悬浊液浊度通常是通过测定其透光强度来确定的，因此其浊度大小取决于单位体积悬浊液内杂质颗粒数目及颗粒的光散射特性。对单一粒径组成的悬浊液，假设单位体积悬浊液中有N个颗粒，颗粒的光散射截面为C；则当一束光通过长度为L的悬浊液的透过光强度I为：
　　　　I=I_Oexp(-NCL) 　　　　 （1）
　　式中I_O为入射光强。式（1）即为Lambert－Beer定律。
　　浊度τ_u的定义为：
　　　　τ_u=NC　　　　　　（2）
　　由式（1）、式（2）得

　　　τ_u=(1/L)ln(I₀/I)

　　浊颗粒的光散射截面C，可用颗粒的几何横截面积表达，对于球形颗粒其表达式为：
　　　　C=Qπα²　　　（3）
　　式中：α－球形颗粒半径；
　　　　　Q－颗粒光散射系数（无量纲），其主要取决于光波长、颗粒大小及折光率。某些特殊情况下，Q可以简单地计算出。
　　对有粒径分布的悬浊颗粒，式（2）变为：
　　　　τ_u=∑N_iC_i
　　式中：N_i－i种颗粒的个数浓度；
　　　　　C_i－i种颗粒的光散射截面。

　　1.2 悬浊液浊度变化理论
　　1.2.1 悬浊颗粒个数浓度的变化
　　连续式浊度计测量浊度时，即使同一个水样其浊度测定值也随机波动，原因是水样的不断更新，导致光路内颗粒个数浓度的随机变化。
　　悬浊颗粒个数浓度N的这种随机变化，主要是由两方面的原因引起的，一是悬浊液中颗粒作布朗运动，使单位体积内颗粒数目产生随机变化，并且该随机过程可以用泊松分布描述。若单位体积内颗粒的平均个数为γ，则实际测量的颗粒数目为η的概率为：
　　　　p(n)=exp(-γ)·γⁿ/n!
　　泊松分布的均值与方差相等，即悬浊颗粒数目的均值与方差均为γ，标准偏差为γ^1/2，并且γ值较大时（γ＞50），分布基本对称并能以高斯分布估计。二是由于悬浊液中杂质颗粒浓度分布的不均匀性引起单位体积内颗粒数目的随机变化，其随机过程也可以用泊松分布描述。
　　对一定体积悬浊液中颗粒数目变化检测的难易程度，在很大程度上取决于检测样品体积的大小，取样体积越大，颗粒数目相对变化越小，越不易检测；相反，取样体积较小时，颗粒数目相对变化值较大，测定较容易。对一般的悬浊液，假定每单位体积内的颗粒数目N为10⁸个/cm³，从一个混合良好的悬浊液中连续取1cm³的样品，则由于样品中的颗粒数目的变化遵循泊松分布，所以上述1cm³的连续样品中，颗粒的平均数目为10⁸个，标准偏差为10⁴，样品中含有的颗粒数在10⁸±2×10⁴之间的概率为95％。这个差异仅为平均值的0.02％，不易检测到。然而，如果取很小的样品体积，如0.1mm³，则样品中颗粒数目的均值为10⁴个，标准偏差为100，连续的样品中的颗粒数目在均值上有±2％的差异，这就很容易检测到。
　　1.2.2 悬浊液浊度的变化
　　悬浊液透光率的变化如图1所示。一狭窄光束照射流动的悬浊液，透过光强由光电管接受并转换成电压信号。

　　由于光路中的颗粒使光产生散射（也可能是吸收），导致透光强度减弱。若光路长为L，光柱的有效面积为A，检测水样的体积为AL，则光路内颗粒的平均个数γ＝NLA，则由式（１）得透光强度的表达式为：

I/I₀=V/V₀=exp(-γ·C/A)　　　　　(4)

　　式中：I－平均透光强度；
　　　　　I_O－入射光强；
　　　　　V/V_O与I/I_O相对应；
　　　　　V_O－相应于入射光强度的电压；
　　　　　V－相应于平均透光强度的电压（直流）。
　　由于光路内的悬浊液不断更新（流动的水样），颗粒数目随机变化（泊松分布），所以透光强度相应随机脉动（参见图1）。透光强度的这种变化可以用透光强度脉动值的均方根表示，相应的电压脉动值的均方根为V_R；其大小与光路内颗粒数目及其大小的随机变化情况有关。
　　假设颗粒数目的随机变化遵循油松分布^[3]，并且光柱内颗粒数目在均值上下一个标准偏差内波动。则通过计算光柱内颗粒数目的上限和下限值对应的平均电压V，即可计算得到V_R。计算时认为上限电压与下限电压之差是实际电压变化的标准偏差的2倍，于是由式（4）得：
　　　　V_R=V_O[exp(-γC/A)](γ^1/2C/A)
　　　　　=V(γ^1/2C/A)　　　　　　　　　　　　　　　　　　(5)
　　对于低浊悬浊液，V≈V_O，则式(5)简化为：
　　　　V_R=V_O(γ^1/2C/A)
　　1.2.2.1 颗粒个数浓度对V_R的影响
　　式(5)用颗粒个数浓度(N)表达为：
　　　　V_R=V_O[exp(-NCL)](NL/A)^1/2·C　　　　　　　　　　(6)
　　对给定的装置，L/A为常数，对颗粒个数浓度N很小的悬浊液，exp(-NCL)≈1，这时V_R只与N^1/2及颗粒大小(通过光散射截面C反映)有关，对固定大小的颗粒而言，V_R随颗粒的个数浓度的平方根成比例变化（图2）。当N较大时，exp(NCL)开始对V_R有影响。当指数部分减小的速度大于N^1/2增加的速度时，V_R达到最大值，对应的颗粒个数浓度Nmax=1/2CL这时V/V_O=0.607。浓度继续增大，V_R开始减小。直流电压V按指数规律随N增大而减小（如图2）。

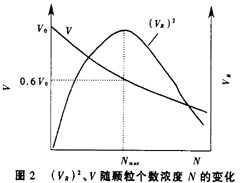
　　综合式（4）和式（6）有
　　　　V_R/V=(NL/A)^1/2·C　　　　　　　　　　　　　　　　（7）
　　等式左边是脉动电压与平均电压的比值，该比值随颗粒个数浓度的平方根不确定地增加，其具体特性，很大程度上依赖于颗粒的特性（C值）。应用中将该比值用R表示，该比值不受取样管管壁污染及电子元件漂移的影响，受影响的只是与平均透光强度对应的平均电压V。
　　1.2.2.2 颗粒大小对V_R的影响
　　为了讨论颗粒大小对V_R的影响，做如下假设：①悬浊颗粒体积浓度为S_V；②悬浊颗粒为单一粒径组成；③颗粒为球形，半径α0则N=3S_V/4πα3结合式（3）和式（7）有

　　式（8）中，设S_V=10-3，A=3.42×10-2mm-2，L=1mm，光波长820nm，悬浊颗粒选聚苯乙稀，Q可根据mie理论计算，则按式（8）即可计算得到V_R/V与颗粒粒径的关系（图3实线）。

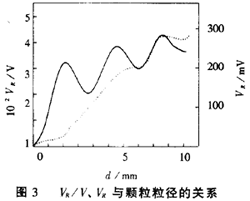
　　图3中V_R/V随粒径增大迅速增大，但出现一系列间隔规则的极大值和极小值，不过总的趋势是V_R/V随粒径增大而增大。
　　图3中的虚线为V_R的计算结果。这里
　　　　V_R=V_O[exp(-3QS_VL/4α)]×（3πS_VL/4A）^1/2·a^1/2·Q　　　　　　　　　（9）
　　由图3可见V_R随粒径增大有规律地增大，曲线波动较小。这主要因为式（9）比式（8）附加了浊度及其随颗粒大小变化一项。
　　对实际有一定粒径分布的悬浊颗粒而言，式（7）变为：
　　　　R=V_R/V=(L/A)^1/2·(∑N_iC_i²)^1/2　　　　　　　　　　　　　　　　　　　　（10）
　　式中N_i是散射截面为C_i的颗粒个数浓度，求和是考虑了各种大小颗粒的综合影响。
　　较小粒径的颗粒，其散射截面较小，相应的N_iC_i²值也较小；而较大颗粒的光散射截面相对较大，即使其颗粒浓度较低，但也能得到较大的N_iC_i²值，对R值的贡献相对要大些，所以，式（10）中R值的大小主要由颗粒的大小决定。在悬浊液中若有少量大颗粒杂质或悬浊颗粒产生絮凝时，由于大颗粒的存在或絮凝的形成会使R值显著增大，因此，R值可作为反映悬浊颗粒混凝程度的指标。
　　当颗粒粒径连续分布时，式（10）中的N_iC_i²项可用积分代替。假设不同粒径颗粒数目的随机变化是不相关的，并且都遵循泊松分布，则颗粒个数浓度脉动的总方差恰好就是每种粒径颗粒单独方差之和，于是对粒径分布为f(a)的悬浊液，式（10）变为：
　　　　R=V_R/V=(N·L/A)^1/2π[∫₀^∞α⁴f(α)Q²(α)dα]^1/2　　　　　　　　　　　　（11）
　　式中N同前，Q(α)是半径为α的颗粒的光散射系数。
　　1.2.2.3 颗粒凝聚或絮凝对V_R的影响
　　悬浊液中颗粒产生凝聚或絮凝时，一方面，悬浊颗粒数目会减少；另一方面，其光散射截面增加。这两种变化对V_R和R有相反的影响，不过颗粒个数浓度的变化比聚集状态的变化对V_R和R的影响要小得多。
　　为了说明这一点，考虑两个简单的颗粒凝聚模式（如图4所示）

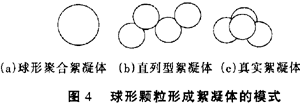
　　第一个模式，假设球形颗粒凝聚后形成更大的球形絮凝体^[图4(a)]，光散射截面假设与颗粒的几何截面积成比例，则
　　　　C_j＝j^2/3C₁　　　　　　　　　　　　　　（12）
　　式中：C_j—j重絮凝体的光散射截面；
　　　　　C₁—初始颗粒的光散射截面。
　　第二个模式，假设球形颗粒凝聚后形成直列形絮凝体^{[图4（b）]}，则其总散射面积就是组成该絮凝体的那些初始颗粒各自散射截面积的总和
　　　　C_j＝jC₁（13）
　　不过，对许多情况，这些假设是不真实的，但它们可以作为极端情况，真实絮凝体的情况介于它们之间^{[图4（c）]}。
　　初始为单一粒径组成的悬浊液在凝聚时可产生一系列粒径的絮凝体，其分布情况取决于凝聚条件。为便于说明，假设絮凝体粒径分布可用Smolu－chowski式表达，则在不同的无量纲时间t/t_f（t为絮凝时间；t_f为颗粒浓度减少到初始值的一半时的时间）值下可算得各种絮凝体浓度，将该计算值和式（12）或式（13）一起代入式（10）就可求出相应的R值。
　　未絮凝时，单一粒径组成的颗粒，其R值可表达为
　　　　R_未絮＝（L/A）^1/2·N0^1/2C₁ （14）
　　对絮凝时有一定粒径分布的絮凝体有
　　①颗粒形成球形絮凝体
　　　　R_絮=R_未絮{∑[(t/t_f)^j-1/(1+t/t_f)^j+1]·j^4/3}^1/2　　　　　　　　　　　　（15）
　　②颗粒形成直列形絮凝体
　　　　R_絮=R_未絮{∑[(t/t_f)^j-1/(1+t/t_f)^j+1]·j^4/3}^1/2　　　　　　　　　　　　（16）
　　用相似的方法可由式（4）推导出悬浊颗粒按上述两种假设模型絮凝时，各自在絮凝前后浊度值变化情况的表达式。图5为两种假设模型各自的R_絮/R_未絮和τ_u絮/τ_u未絮随絮凝进行其变化情况的计算结果。

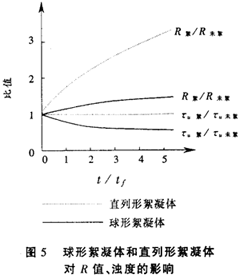
　　对形成直列形絮凝体的假设，凝聚发生后，浊度不变化，因为这时絮凝体散射的光与初始颗粒散射的光相同，但此时R值显著增加；对球形聚合假设，当颗粒凝聚时，浊度明显降低，而R值却有相当比例的增大。
　　图5中所示的两种凝聚假设条件下的R值相对变化曲线是两种极端的絮凝情况。实际中普遍存在是随机形成的絮凝体，其R值变化曲线应介于这两条曲线之间。由此可见，无论絮凝体的结构如何，当发生絮凝时人值总是增大的。

2 悬浊颗粒粒径分析

　　式（4）两边取对数，并用N描述

ln(V₀/V)=NLC　　　　　　　(17)

　　由式（7）和式（17）消去颗粒的光散射截面C（颗粒的复杂函数），可求得悬浊颗粒个数浓度

　　若颗粒的体积浓度S_V已知，则由式（18）可求出颗粒等体积球半径α

　　式（19）只适用于单一粒径组成的悬浊液。
　　对于具有一定粒径分布的悬浊颗粒^{[其粒径分布函数f(a)]}，结合式（3），式（17）可改写为

　　由式（11）、式（20），即可得到具有一定粒径分布的悬浊颗粒的个数浓度

　　同样，若悬浊颗粒体积浓度为S_V，则由式（21）可求出悬浊颗粒的平均体积粒径α。

　　总之，对单一粒径组成的悬浊液，颗粒个数浓度N可由悬浊液透光脉动检测装置方便地测出，而不需要知道颗粒的任何光学特性，尤其当颗粒体积浓度S_V已知时，可定量计算出平均体积粒径。对具有一定粒径分布的悬浊颗粒，由该装置也可以半定量地得到悬浊颗粒的个数浓度及其平均体积粒径。

3 结论

　　透光脉动悬浊颗粒检测技术与以往其它光学检测法有本质的区别。透光脉动法重点考察的是悬浊液透光率的脉动值，并且该值通过光电转换可以用输出电压的脉动值的均方根V_R或R（R=V_R/V）表示。悬浊液透光率脉动值V_R或R（R=V_R/V）主要与悬浊颗粒大小有关，颗粒个数浓度对V_R或R的影响较小。对单一粒径组成的悬浊液，由透光率脉动值可以定量地计算出颗粒的个数浓度和颗粒粒径，而不需考虑颗粒的任何光学特性。对于具有一定粒径分布的悬浊液，则必须考虑粒径分布函数。对悬浊颗粒的各种凝聚模式的分析结果表明，悬浊颗粒凝聚（或絮凝）总是使透光脉动值增大。由于比值R不受取样管管壁污染及电子元件漂移的影响，受影响的只是与平均透光强度对应的平均电压V，所以实际应用中可将R值作为检测指标。

参考文献：
　　[1]Kayode T O，Gregory J A.New technipue for monitoring alum－sludge conditioning[J].Wat.Res.，1988.22(1)：85～90.
　　[2]Bryant R L.On－line control of coagulant dosage using the streaming current detector[J].Industrial Water Engineenng，1983,20(5)：16～36.
　　[3]Gregory J.Turbidity Flctuations in flowing suspenslons[J]．Colloid Interface Sci.，1985，105(2)：357－371.

　　作者简介：
　　于水利（1962－），男，教授，博士生导师，哈工大市政工程系主任。1962年10月生，1983年毕业于哈尔滨建筑大学市政与环境工程学院，长期从事给水排水、环境工程的教学和科研工作。
　　Email：ysihgdd@china.com
　　收稿日期：2000-10-16

　　＊霍英东教育基金会青年教师基金(编号：070)，湖北省废物地质处置与环境保护重地实验室开放研究基金联合资助。