遗传算法在供水管网改扩建优化设计中的应用研究
戴雄奇
(深圳市自来水集团有限公司供水调度中心)
摘 要 本文首先简要介绍了遗传算法的基本思想和步骤:继而探讨了如何将遗传算法应用于求解供水管网改扩建优化设计问题,并提出了对连续/离散混合变量的编码方法;最后将遗传算法应用于一个供水管网改扩建实例,效果比较明显。该算例表明该算法具有很强的适应性,可实际应用于管网改扩建优化设。
关键词 遗传算法 供水管网 改扩建优化
1 引言
城市供水管网改扩建优化设计是基于对现有管网的工况正确分析、评价的基础上进行的,由于供水管网改扩建设计是一个复杂的多元系统,不仅目标函数比较复杂,受许多因素的影响和制约,而且优化设计模型中加压泵站的水泵台数为整型变量,管道管径为离散型变量,是一类混合离散变量优化问题。
对于供水管网改扩建的优化设计的求解,到目前为止,国内外学者已经提出了不少方法,这些方法均使用数学规划技术寻找最优解。不少方法假定,设计变量是连续的,且目标函数具有可导性,但实际上,混合离散优化问题的特殊性使这些求解方法往往难以获得原目标函数真正的最优解。为外,该问题也是一个非线性规划问题,非线性规划至今没有一个成熟算法,即使有些方法,当被用于供水管网改扩建优化设计问题时,往往收敛到局部最优解,很难收敛到全局最优解。为了克服数学规划方法用于管网改扩建优化设计所带来的缺陷,本文提出了一种人工智能性算法,即含有交叉和变异等算子的遗传算法。
2 遗传算法的基本思想
遗传算法(Genetic Algorithm, GA)是基于人类补会的进化过程,它首先利用随机力式在个空间内产生一初始群体(祖先),即多个初始点,群体中每个个体称为染色体,它对应有优化问题的一个可能解,染色体的最小组成元素就称为基因它对应可能解
某一特征,即设计变量。染色体的评价函数值反映可能解的优劣,按照优胜劣汰原则对染色体进行选择,相对“好”的个体得以繁殖,相对“差”的个体将死亡,因此群体整体的性能,通过选择、杂交、突变等过程将趋于改善,经过若干代繁衍进化就可使群体性能趋于最佳[1]。
2.1 遗传算法的基本步骤
(1)编码:二进制编码方法是遗计算法中最常用的一种编码方法,它使用的编码符号是由二进制符号O和1所组成的二值符号集{0,1},它所构成的个体基因型是一个二进制编码符号串。二进制编码符号串的长度与问题所要求的求解精度有关,假设某一参数的取值范围是[Umin,Umax],用长度为λ的二进制编码符号串来表示该参数,它总共能够产生2种不同的编码。
二进制编码的编码精度为:δ=[Umax-Umin]/2λ-1
假设某一个体的编码是:X:bλbλ-1bλ-2∧b2b1
则对应的解码公式为:x=Umin+[![]() bi.2i-1).[lUmax-Umin]/[2λ-1]
bi.2i-1).[lUmax-Umin]/[2λ-1]
(2) 产生初始群体:由计算机按随机方法从可能解中产生给定数量的二进制代码串,构成一个原始的祖先群体,其中的每个二进制代码串代表了这一群体的一位祖先,对每位祖先(可行解)计算其相应的函数值F1。按F1的大小来评价这位祖先的染色体的素质。
(3)计算适应度函数:最优化问题可分为两大类,类为求目标标明函数的个局的最大值,另一类为求目标函数的全局最小值。对于这两类优化问题,由解空间中某一点的目标函数值f(X)到搜索空间中对应个体的适应度函数值F(X)要通过适当的方法加以转换。在遗传算法中,群体的进化过程就是以群体中各个个体的适应度为依据,通过个反复迭代过程,不断地寻求出适应度较大的个体,最终就可得到问题的最优解或近似最优解。
(4)选择:这一步模拟生物进化的自然选择功能。从原始群体中随机取一对个体作为繁殖后代的双亲,选种的规则是适应度值Fi越大的个体,赋予的选择概率Pc越大,一般P1∝Fi即适应度值高的个体有更多的繁殖后代的机会,以使优良特性得以遗传和保留。
(5)交叉:遗传算法中所谓交义,是指对两个相互配对的染色体按某种方式相互交换某部分基因,从而形成两个新的个体,它以一定的概率Pc在个体编码串中随机设置一个交义点,然后在该点相互交换两个个体的染色体。
(6)变异:突变是用来模拟生物在自然的遗传环境中,由于各种偶然因素引起的基因突变,即将个体染色体编码串中的某些基因值用其他等位基因来替换,从而形成个新的个体。
综上几步:通过选择、交叉、变异得到的新一代群体,将替代上一代群体,一般说来新的群体的平均素质可望比上一代群体素质要好。不断重复迭代上述过程,各代群体的优良基因成份逐渐积累,群体的平均适应度值和最优个体的适应度值不断上升,直到迭代过程收敛(适度值趋于稳定)即找到了最优解。
3 遗传算法在供水管网改扩建优化设计中的应用
3.1 城市供水管网改扩建优化设计数学模型
改扩建管网,由于新旧设施共存,各部分相互牵连、互相影响,构成一个复杂的大系统,凭经验的定性分析无法保证管网系统设计的质量,只有建立切合实际情况的数学模型,通过科学计算才能取得较合理的管网设计方案。供水管网改扩建优化设计的目标,就是在供水管网系统改扩建优化设计基本思想指导下,以有限的建设资金最大限度地提高改扩建管网供水的综合效益,即在满足水量水压要求的前提下,推求改扩建管道建设费用及改扩建后整个管网系统运行动力费用最低的纤济管径[2]。
其数学模型为:
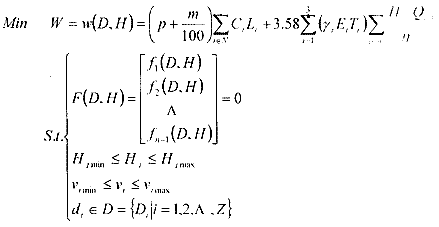
式中:p——管网造价动态折算系数;m——大修基金提存率(%);
N——新铺设管段集合;Ci——第i条管段的单位长度造价(元/米〕;
Li——第i条管段的长度(米);γi——用电i期供水能量变化系数;
Ei——用电i期电费价格(元/千瓦时);Ti——用电i期供水时间(小时);
ns——泵站个数集合;Hi,j——第j个泵站机组i供电期的扬程(米);
Qi.j——第j个泵站机组i供电期的输水量(升/秒);
η——第j泵站机组i供电期的泵站效率(%)。
3.2 用遗传算法求解供水管网改扩建优化设计问题
某城市现状供水管网经简化后,共有67条管段(管径均大于等于DN300),有55个节点(其中有2个水源点)。由于城市生产、生活用水的增长,需将原管网进行改扩建,经有关部门规划,需增设23个节点,31条管段。
用编制的遗传算法程序对管网进行优化计算。按程序要求,需准备如下数据:
p=0.18;m=3%;γ=0.5; E=0.8;η=0.8;N=31;ns=2;Dmax=1000mm;
vmin=0.6m/s;vmax=1.5m/s;Hmin=18.00m;Hmax=50.00m。
然后用遗传算法进行求解,求解时注意以卜两个问题:
(1)编码问题。采用二进制编码方式,对于管径编码时,取范围在[300,1000]内的标准规格的管径,δ取100,则由δ=Umax-Umin/2λ-1得λ=3,即染色体上每三位表示一个标准规格管径;对于节点水压编码,其范用是[18.00,50.00],若精度δ取0.1,则由δ=[Umax-Umin]/[2λ-1]得λ=8.4≈9,此时精度为0.06。山于共有31条新建管段,78个节点,所以整条染色体长度为:3×31+9×78=795。
(2) 适应度函数问题。将要求解的数学函数和约束进行变形和转换,通过引入惩罚函数的方法化成遗传算法的标准适应度函数。原数学模型可变为:
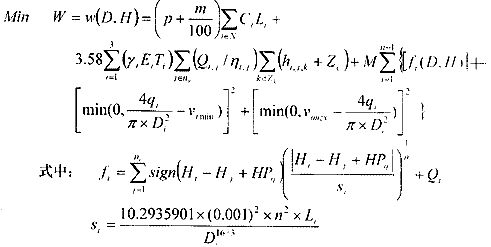
将目标函数化为无约束极大值形式为:Max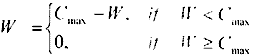
式中,Cmax为一个适当地相对较大的数。本例中,M取5.0e+5,Cmax取5.0e+7。优化结果与规划结果的比较见表一:
表一 管径优化结果和规划结果的比较
序号 规划(mm) 优化(mm) 序号 规划(mm) 优化(mm) 1 800 500 17 500 1000 2 800 600 18 600 400 3 700 900 19 600 300 4 600 700 20 800 600 5 800 300 21 800 900 6 400 700 22 800 400 7 500 400 23 800 800 8 800 800 24 800 800 9 800 300 25 600 400 10 400 1000 26 400 500 11 600 400 27 500 400 12 400 400 28 600 300 13 400 900 29 600 400 14 600 500 30 600 700 15 600 900 31 600 500 16 600 300表二 规划管网与优化管网的比较
管网状况 新建管段造价年折算值(万元/年) 管网年运行费用(万元/年) 管网年费用值(万元/年) 规划管网 2595.36 487.33 3082.69 优化管网 2119.01 496.81 2615.82
从表二可看出,优化计算后的每年费用比预计规划计算的节省了400多万元,大大地减少了管网的投资费用,故能产生较大的经济效益和社会效益。
4 结束语
综上所述,用遗传算法求解供水管网改扩建优化设计问题得到的结果是令人满意的,这说明遗传算法是一种比较好的搜索算法,它不仅快速、准确、搜索遍及全空间,具有较大的把握得到全局最优点,而且不用对原问题作过多的分析处理,具有很高的适应性。当然遗传算法也存在一些缺点,如遗传算法的操作参数和优化结果相互之间比较独立,故对于操作参数的选取比较困难;此外由于遗传算法还处于发展的初级阶 段,尚有许多问题需要研究和探讨,比如对于大型复杂的问题收敛速度还比较慢等等[3]。
总之,本文采用遗传算法求解直接优化调度数学模型获得了较理想的结果,故认为遗传算法在管网优化方面的应用值得推广。
参考文献:
1.周明、树栋,《遗传算法原理及应用》,国防工业出版社,NO.1,1999
2.赵运德,用广义简约梯度法求管网经济管径,水利学报,No.6,1999
3.王平洋,加快遗传模糊算法的搜索过程,电网技术,Vol.23,NO.5,1999
论文搜索
月热点论文
论文投稿
很多时候您的文章总是无缘变成铅字。研究做到关键时,试验有了起色时,是不是想和同行探讨一下,工作中有了心得,您是不是很想与人分享,那么不要只是默默工作了,写下来吧!投稿时,请以附件形式发至 paper@h2o-china.com ,请注明论文投稿。一旦采用,我们会为您增加100枚金币。








