反应池中颗粒惯性作用的影响分析

徐立群，王芳，何钟怡?
(哈尔滨工业大学市政环境工程学院，黑龙江哈尔滨　150090)

　　摘 要：从颗粒在流场中的运动方程出发，研究球形颗粒在流场中的跟踪特性和频率响应，证明惯性作用是导致反应池内颗粒碰撞的重要原因，并给出影响惯性作用的主要因素，据此对反应池某些现象进行了理论解释。
　　关键词：惯性作用；絮凝；频谱分析；球形颗粒
　　中图分类号：TU992
　　文献标识码：C
　　文章编号：1000-4602(2002)03-0044-04

　　反应池中颗粒的絮凝过程存在多种碰撞凝聚的机制。在凝聚的初始阶段水中颗粒的尺度很小，能够很好地跟随流体运行，流场中局部速度差异导致的梯度凝聚起着重要作用。随着颗粒尺度不断增大，颗粒跟随特性将不断恶化，即使在局部均匀的流场中，因絮凝颗粒的尺度和密度不同也会产生颗粒速度差，形成追赶碰撞，这种现象称为惯性效应。从絮凝的全过程考虑，这种惯性效应可能起着相当重要的作用。?

1 　粒子对流场的跟随特性及频谱分析

　　首先来研究最简单的例子。假设半径为α的球形粒子处于一维非恒定流场中，粒子的存在将会影响流场的局部，但距离粒子稍远处的流场不受粒子干扰，其速度为v(t)； 球形粒子受流场影响，其速度为u(t)，t为时间。由于粒子不会与流场完全同步运动，v(t)与u(t)不相等，流体绕球体运动产生作用力F，根据牛顿定律：?
?　　F=m(du／dt）　　　(1)?
?　　m=（4／3）πα³ρα?　(2)?
　　式中m——球体质量?
?　　　ρα?——球体密度?
　　由于所研究的粒子尺度很小，绕流运动的雷诺数亦非常小，故可视为stokes型非恒定球体绕流。作为流体力学的经典成果，该作用力F已经求得［1］，表达式为：?

　　

　　式中 ?ρ——流体密度?
?　　　　γ——流体的运动粘性系数?
　　将式(3)代入式(1)，得到粒子的运动方程：?

　　

　　若流场的速度v(t)已知，由式(4)可以求出球体跟随运动速度u(t)。在湍流中v(t)具有一定的随机性，任意指定一种v(t)的形式一般不具代表性。为了从更广泛的意义上认识惯性效应，可以通过Fourier变换表示v(t)。把函数v(t)展开成一系列以时间为变量的具有不同振幅和相位的正弦波和余弦波之和，相应的颗粒速度也展开成Fourier函数，就能够很细致地了解不同v(t)时颗粒的跟随特性。上述方法与常用的Fourier级数很相似，差别仅在于此处各级子波频率是连续变化的，而Fourier级数的子波频率是跳跃变化的。根据定义：?

　　

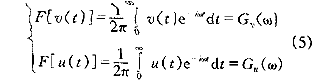
　　Gv(ω)和Gu(ω)分别为v(t)和u(t)的Fourier频谱，它是一个复数。当把函数展开成一系列子波之和时，G(ω)的模｜G(ω)｜是频率为ω 的子波的振幅，其幅角arg［G(ω)］为该子波的相位。?
　　对式(4)进行单边Fourier变换，并进行整理得到：?

　　

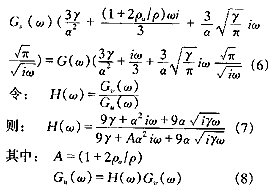
　　式(8)表明，频率为ω的流场子波将引起粒子作同频振动，但流场子波的振幅与流场粒子的振幅并不一定相等，相差一乘积因子H(ω)。H(ω)的模和幅角反映了 粒子对流场的跟随特性，称之为传递函数(跟随函数)，表示把流场振动传递给粒子的强弱程 度。若｜H(ω)｜=1，则v(t)和u(t)的各子波振幅相等，即粒子的跟随特性很好，反之｜H(ω)｜≈0，则｜Gu(ω)｜=0，表示粒子不存在该子波的振动，即完全不跟随流场运动。?
　　由式(7)求得跟随函数H(ω)的模｜H(ω)｜和幅角值θ如下：?

　　

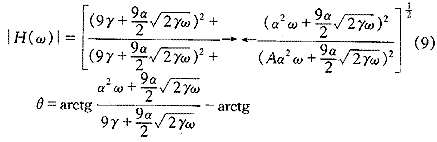
　　通过编制计算程序，可以求得｜H(ω)｜和θ。特别是｜H(ω)｜更能反映出颗粒运动速度与流场速度的差别。绘制T=20℃、密度ρ=5000kg/m³的颗粒处于 水中时，｜H(ω)｜随频率的变化曲线如图1。?

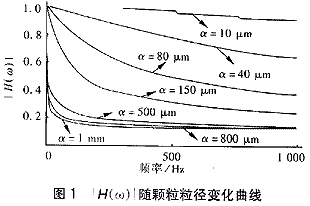
　　由图1可知，①颗粒粒径α一定，｜H(ω)｜随ω的增加而减少。即在低频部分粒子跟踪能力强，随频率增加，跟踪能力显著下降。②随粒径α的增加，｜H(ω)｜减小，颗粒跟随性变差，说明惯性作用随粒子半径的增大而增强。
　　在相同流场波动频率下，相对而言小颗粒跟随性好，大颗粒跟随性差，颗粒粒径相差越大，颗粒之间速度差越大，而随波动频率的增加，大小颗粒的跟随性将同时变差，对不同的波动频率,大颗粒｜H(ω)｜减小的速率较小颗粒快,也就是说流场频率的增加将导致惯性 效应增强,使颗粒速度差增大，更加容易形成颗粒之间的追赶碰撞。?
　　由H(ω)表达式可知，影响惯性作用及颗粒跟随性的主要影响因素有γ(和水温有关)、颗粒粒径α、波动频率ω及粒子的密度，即H(ω)～(γ，α，ω，ρα/ρ)，因此对相同性质的颗粒，其跟随性因颗粒粒径和密度不同而具有很大的差异，将导致颗粒之间产生速度差，为颗粒之间的相互接触碰撞提供条件。?

2 给水处理反应池中惯性作用的影响

　　从絮凝的整个过程来看，反应过程是一个絮凝颗粒不断长大和流动速度梯度沿流程降低，同时发生颗粒碰撞、长大及剪切分散的复杂物理化学过程。反应条件要求随反应的进行，反应池流速逐渐降低以防止矾花颗粒的破碎。此时流场平均速度梯度逐渐减小，平均局部速度梯度也降低，为颗粒碰撞提供的动能减少。由颗粒间的作用力分析已经知道两个颗粒碰撞时必须具有一定的动能以克服颗粒间的排斥能峰，因此流场局部速度梯度所导致的颗粒碰撞次数将减少，同时有效碰撞次数降低，这对反应是不利的。按常规设计的反应池为了保证颗粒碰撞总的次数，需在反应池中后段保证较长的反应时间。?
　　另一方面，由于在反应池的任一阶段颗粒都是相对的大颗粒和小颗粒共存，呈一定的量级分布。在未投加絮凝剂时颗粒量级差别不大，基本在胶体量级；随反应的进行，最大颗粒和最小颗粒的尺度差将增大，在反应池末端最大颗粒尺度可达到mm量级，而最小仍为胶体量级，它们的跟随函数值在图1已经给出。随反应的进行，颗粒平均尺度增加，颗粒的跟随性降低很快，惯性作用导致的大小颗粒之间的速度差将增大，并足以为大小颗粒之间的碰撞提供动能，惯性作用导致的颗粒碰撞和有效碰撞次数将增加。在普通的反应池中，池末端的流场平均波动频率较低，惯性作用所起作用有限，所以需要的反应时间较长。如果在反应池内通过各种手段来合理地提高流场波动频率，加强惯性作用，将有可能使反应效果得到加强，提高反应效率，缩短反应时间。?
　　近年来针对反应过程所做的研究工作可以说明上述理论分析结果。通常在反应池的设计中，用反应时间和G值或GT值来控制设计参数，除此之外还必须考虑反应池内的水力分级和能量损失。在G值基本上处于同一量级的情况下，一般通过增设弯道(如网格反应 池)、在反应池流道内放置扰流装置如格栅或栅条等、改变流道的尺度(如波纹板反应池) 使水流强烈地旋转(如旋流反应池和孔室反应池及机械反应池)或脉动来改进反应效果。这些改进使在反应池内达到理想效果的反应时间由0.5h缩减到目前的8min，甚至更少。此时整个反应池的平均速度梯度较无扰流装置基本没有改变，这些反应池的改进工作无法仅用速度梯度理论给出合理的解释。从流体力学的角度来观察上述反应池结构上的改进可以看到一个共同点：通过改变流动状态、增加平均水流的扰动来改进反应效果，它的实质是增加了湍流的高频分量。前面的理论计算，｜H(ω)｜～(γ，α，ω，ρα/ρ)说明惯性作用产生的颗粒速度差对大小不同的颗粒在流场频率变化时提供的力的作用情况不同。较高流场频率将导致较高的大小颗粒速度差，提高颗粒碰撞次数。增加湍流中的高频分量，更充分地利用了惯性作用，从而提高了反应效率。这说明高频分量是通过惯性起作用的，惯性效应是使反应过程得到加强的基本因素。?
　　惯性作用原理还能对反应池内几个典型的现象进行解释：?
　　① 温度和粘性对于反应的影响?
　　取颗粒密度为5000kg/m³,颗粒尺度为100μm，计算水温为0℃(γ=1.787×10^-6m²/s)、10℃(γ=1.004×10^-6m²/s)和20℃(γ=1.004×10^-6m²/s)时颗粒跟随函数的模和幅角(如图2)。?

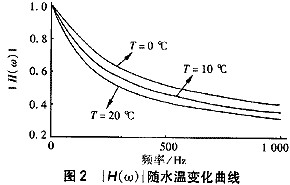
　　由图2可知，3条曲线反映了随水温的升高，颗粒的跟随性变差；随水温的降低，水的粘性增加，颗粒跟随性变好。在水温低时由于惯性作用导致的颗粒碰撞减少，反应效果变差而难于处理。为处理低温水必须进一步增加水流的高频部分以增强处理效果，而一般的水处理设备不具备随温度变化调节水流的能力，惯性作用在处理低温、低浊水时强度又不够，所以对夏季高温水处理效果理想，而对于低温、低浊水就不能达到理想的处理效果。只有按冬季最不利情况设计的水厂(反应时间比较长或设计流态结构惯性作用较强)才能在任何时候都得到满 意的水量和水质。?
　　② 有机污染水及高藻水的处理?
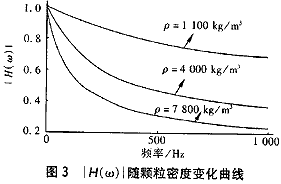
　　若不考虑有机污染水化学上的特性，它和高藻水在处理上有共同的难度，除了这两类水形成的矾花颗粒比较轻、难于沉淀这个难题之外，在反应池还难于形成理想的矾花颗粒，这主要 是由于有机物和藻类密度比较低，惯性作用比较弱的缘故。颗粒密度对于惯性作用的影响见图3。
　　显而易见，颗粒密度大则惯性作用强，颗粒密度小则惯性作用弱。江河水质以泥砂为主，杂质颗粒密度较大、惯性作用强，同样反应条件下碰撞次数多，“有效碰撞”次数也相应增加，所以江河水较水库水易于处理，对构筑物设计要求比较低。?

3 需要说明的问题

　　① 由于湍流的复杂性，目前还无法知道湍流中各点确切的平均速度梯度分布情况和它所导致的颗粒碰撞数，计算惯性作用导致的颗粒碰撞数也还有待于进一步研究，因此还不能确切 给出惯性作用在什么范围是最重要的。
　　② 实际研究颗粒碰撞时应当考虑复杂的物理化学作用力的影响。文中只简单地 把力的作用影响认为是在颗粒周围形成一个力的作用半径，两个颗粒之间发生有效碰撞只需克服颗粒之间的作用力，使一个颗粒进入另一个颗粒的作用半径之内。
　　③ 颗粒形状假设为球形，忽略了颗粒形状以及颗粒旋转的影响。

4 结语　

　　分析流场中的颗粒受力出发，认为惯性作用是影响流场中颗粒碰撞的因素之一，采用Fourier频谱分析的办法，建立了非恒定流场中的颗粒运动方程，并建立和求解了颗粒的跟随函数，指出影响颗粒跟随性的主要因素是流场频率、颗粒尺度和密度以及流体的运动粘度。在此基础上提出：适当增加流场的扰动以增强高频分量可以改进反应效果，并对反应池中低温和高藻水的难处理现象从惯性作用角度进行了分析。

参考文献:

　　 ［1］ 许保玖，安鼎年.水处理理论与设计［M］.北京：建筑工业出版社，1989.

---

　　电　　话：(0451)2373279?
　　传　　真：(0451)6282109?
　　E-mail:dxzx@fm365.com?
　　收稿日期：2001-11-01