节点递归算法用于污水管网的优化设计

伊学农，刘遂庆
同济大学环境科学与工程学院，上海200092

　　摘　要：采用节点递归算法和坐标轮换法，以节点为研究对象，以费用最低为优化目标，直接以节点标高为约束条件对污水管网的设计进行了优化。管网联系矩阵的应用克服了在管网交叉节点处上下衔接的计算和控制点不易确定的困难。最后，列举实例进行了计算说明。
　　关键词：污水管网；优化设计；节点递归算法
　　中图分类号：TU992.02
　　文献标识码：C
　　文章编号：1000-4602(2002)10-0058-03

　　目前，多数污水管网的计算程序没有利用图论和矩阵理论来获得和存储管网信息数据，故难以掌握整个污水管网的信息以及节点与管段的衔接关系，在多管段交叉点处也难以通过自动判断和计算确定上、下游管段的有关标高等水力参数，尤其当需对管网中管线交叉节点的标高等其他水力参数进行控制时更是无法进行正常计算。为此，提出以节点为研究对象，采用节点递归算法和坐标轮换法经一次计算即可完成对整个管网计算的优化，并且还可有效地控制某些节点的水力参数。

1　污水管网与图论

　　污水管网可被视为有向图(按污水在管内的流向)，而污水管网定线后则整个管网中所有管段的流量就被确定下来。根据图论，可用一个矩阵表示污水管网节点与管段的衔接关系，当管网图形确定后则管网联系矩阵就被确定下来，反之若已知管网联系矩阵，则可唯一地确定管网图形。在污水管网中由于最终一个节点不再接受流量并且无后续管段，因此在联系矩阵中不再列出。根据污水管网的特点，采用如下规则表示联系矩阵M：

　　

　　为方便起见，采用仅有一个交汇节点的简单污水管网(如图1所示)，则联系矩阵为：

?　　

2　管网流量矩阵计算

　　设图1中各管段的平均流量分别为Q1、Q2、Q3、Q4，则用向量表示如下：
?　　　　　　　Q=(Q1,Q2,Q3,Q4)^T
　　按流量计算原则，各管段服务面积上的流量由各管段的起端进入，在此将各管段流量转化为从各管段流入的节点流量。设各管段服务面积上的本段流量分别为q1、q2、q3、q4，用向量表示如下：
?　　　　　　　q=(q1,q2,q3,q4)^T?
　　按流入节点的流量为负、流出节点的流量为正的原则，对管段流量进行计算。对于图1按节点写出流量平衡方程，即节点方程：

　　

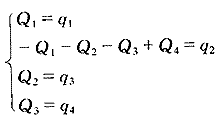
　　若写成矩阵形式，则为：
?　　　M·QT=qT
　　其中，M即为管网联系矩阵，当某节点i与某管段j相连并且该管段的流量从该节点流出时，则M［i，j］=-1；反之，当该管段的流量从该节点流入时，则M［i，j］=1，其余情况下M［i，j］=0。q向量为各管段的本段流量，当管网定线后可直接求出。因此，利用数学方法直接求解即可得出各管段的平均流量Qi(i=1,2,3,4)，再乘以总变化系数即可求出生活污水的设计流量Q_i′。设图1中各管段的集中流量为qj=(qj1,qj2,qj3,qj4)，则各管段的设计流量计算如下：
?　　　　　Qsi=Qi′+qji(i=1,2,3,4)
　　至此，整个管网的设计流量就确定下来。

3　目标费用函数

　　优化污水管网系统的目的是使整个管网在服务年限内的基建投资和经营费用现值的总和(主要包括管网投资和泵站投资及运行费用)为最小。采用如下形式的费用函数：

　　　　

　　 式中CT——整个管网系统总费用的现值，元
?　　　 Li——各管段的长度，m
?　　　 K?——运营费用折算成现值的现值系数?
?　　　 Opj——各泵站的运营费用，元/(座·a)，可取其主要部分(电费)代替
?　　　 m、n?——分别为系统中的管段数和泵站数
?　　　 Ci、Cpj——各管段的单价(元/m)和各泵站的单价(元/座)

4　节点递归算法与水力计算

　　污水管网的水力计算按照重力流进行。以节点为研究对象采用节点递归算法，不仅适用于新建管网的设计，更能适用于多数城市污水管网的扩建工程，尤其适合地下管线交叉多、管线综合较难的污水管网工程的设计等。
　　节点递归算法的步骤如下：
　　①指定计算起始节点。
　　②判断是否为起点管段：若是，则转③继续；否则转④继续。
　　③按起点埋深直接进行水力计算；找出下游节点，转②继续。
　　④判断其上游管段是否计算完毕：若是，则转⑤继续；否则转⑥继续。
　　⑤搜寻该节点上游所有的管段，计算确定该节点所有上游管段中最大埋深或最小管内底标高的管段，并记下其管径和管内底标高，以及最小水面标高、流速等必要的水力参数，找出下游管段并进行水力计算；找出计算管段的下游节点，返②继续。
　　⑥采用坐标轮换法，将计算节点坐标移至当前管段的上游节点，转②继续。最后再沿此逆方向按坐标轮换法，将计算节点移回当前节点进行计算。
　　⑦当所有管段计算完毕，结束。
　　流量和水力计算均采用节点递归算法，计算从上游节点向下游节点的方向进行，遍历管网所有节点和管段。
　　进行水力计算时根据所选管径的大小，按下游管段起点的水面标高和管内底标高均不高于上游计算管段终点相应标高的衔接原则来计算下游管段起点的标高以及其他水力参数，具体计算方法如下：
　　①当计算管段为新设管段时，取较大充满度和较小埋深，以造价最小为目标函数进行优化计算。
　　②当计算管段为原有管段或设计者已确定计算管段起点和终点的管内底标高(或该两点的管顶标高)时，设长度为L、标高分别为?HGi1和HGi2，则以该节点的标高作为控制因素对该管段进行水力计算，其水力坡度I为：
?　　　　　　I=（HG_i1-HG_i2）／L?
　　根据求出的水力坡度，利用下式采用迭代法计算过水断面夹角θ并计算其他水力参数：
　　　　　　　θ=8nQ／［D／4(1-sinθ／θ］^2/3I^1/2D²+sinθ　　　　(2)
　　③当地面坡度较大、管道埋深为负值时，同样可首先确定管段两节点的标高，按以上各式进行计算调整。
　　④对于地势平坦的地区，可按造价最小原则直接进行优化计算。根据水力计算惯例(即下游管段的计算流速不小于上游管段的计算流速)确定下游管段的设计流速v，再利用下式的迭代法计算过水断面的夹角θ，并计算其他水力参数：
?　　　　　　θ=8Q／D²V+sinθ
　　根据计算出的各水力参数判断是否满足规范的约束条件，如果满足则将水力参数值作为计算值保存，并按造价最低原则寻优，以确定全局造价最低并符合要求的管径。

5　程序实现与设计实例

　　根据上述算法，用VISUAL C++语言编写污水管网优化计算程序。程序中的数据输入主要包括交互式、数据文件式等，内容有总管段数、管段编号、起点和终点编号、管段长度、服务面积、人口密度、排水量标准和集中流量以及地面标高、控制节点的管内底标高等，当某节点的管内底标高无需控制时可以不输入，此时按程序设计直接优化。
　　该算法程序可按不同服务区域、不同人口密度和排水量标准分别计算各管段的设计流量，克服了同一主干管服务面积内标准难以划分的弊端。
　　水力计算程序能根据各节点的衔接关系自动检查计算节点上游各管段终点的水力参数，根据设计原则确定下游管段起点的水力标高并进行水力计算；如此，依次循环遍历所有节点，直至计算完所有管段。按此设计，可自动对节点处各管段的标高进行处理，并可一次计算完整个城市污水管网，克服了单条管段计算和节点处需人工调整以及多次重复计算等造成的繁琐和困难，也避免了管网系统中难以确定控制点以及无法人为控制系统中某些节点标高的缺点，并使污水管网的设计更趋合理和优化。
　　根据所编程序，对山东省某县级市的由228个设计管段、管线总长度约计79 km的污水管网系统进行了优化计算，尽管管网中地面坡度在-10%～30%变化，结果还是令人满意的，并且计算所需时间＜1s(PIII-450)。部分计算结果见表1。

表1　部分计算结果 管段 管长(m) 流量(L/s) 管径(mm) 地面标高(m) 管内底标高(m) 造价(万元) 管段 管长(m) 流量(L/s) 管径(mm) 地面标高(m) 管内底标高(m) 造价(万元) 上游 下游 上游 下游 上游 下游 上游 下游 1-2 700 111.83 500 209.000 208.000 207.461 206.317 2.7636 5-7 500 46.86 300 204.700 204.900 203.284 201.778 1.5531 2-4 600 151.27 500 208.000 202.000 206.217 200.600 3.2429 11-10 350 21.01 300 204.500 203.000 203.200 201.700 0.6856 4-9 500 209.8 600 202.000 200.000 200.500 198.500 2.8473 10-9 450 48.31 400 203.000 200.000 200.640 198.700 2.2078 9-14 620 391.61 700 200.000 198.000 197.409 196.200 7.6356 3-2 250 7.37 300 203.000 203.000 201.700 200.950 0.6781 14-15 1000 467.03 900 198.000 192.000 196.200 190.200 10.046 12-13 500 46.35 300 207.500 203.000 206.200 201.700 1.3231 6-7 280 19.43 300 207.500 204.900 206.200 203.600 0.5485 13-14 600 73.41 400 203.000 198.000 201.000 196.700 2.9929 7-4 350 70.23 400 204.900 202.000 201.725 200.700 2.3256 8-9 600 171.59 600 200.000 200.000 198.426 197.709 3.5278

6　结论

　　①利用图论的理论和管网联系矩阵来表达污水管网中节点与管段的衔接关系简化了计算。
　　②采用节点递归算法和坐标轮换法可一次遍历整个污水管网系统。在一定范围内，可对管网中某个或某些节点标高进行控制。
　　③该方法可针对污水管网中不同的排水标准和人口密度等参数的分区进行计算。
　　④采用枚举标准管径法可优化污水管网的造价。
　　⑤该方法同样适用雨水、合流制排水管网系统。

参考文献：

　　 ［1］周玉文，赵洪宾.排水管网理论与计算［M］.北京：中国建筑工业出版社，2 000.
［2］丁宏达.雨(污)水管道系统优化设计［J］.中国给水排水，1988，4(1):51-5 4.?
　　 ［3］彭永臻，崔福义.给水排水工程计算机程序设计［M］.北京：中国建筑工业出版社，1994.
　　 ［4］Magdalene Marinaki,Markos Papageorgiou,Albert Messmer.Multivariable regulator ap proach to sewer network flow control［J］.Journal of Environmental Engineering，1999，125(3)：267-276.
?［5］Simpson AR,Dandy GC，Murphy LJ.Genetic algorithms compared to other technique s for pipe optimization［J］.Journal of water resource planning and management，1994,120(4):423-443.

---

　　电　　话：(021)65988922
　　E-mail:yixn@263.net
　　收稿日期：2002-04-30