一种新型滗水器的排水水力学模型及计算

顾剑峰
(上海船舶运输科学研究所，上海200135)

　　摘　要：介绍了一种新型滗水器，并对其排水过程的水力模型进行了研究，提出了在考虑管道阻力损失的条件下计算滗水器排水流量和排水时间的理论公式，试验证明这些公式是正确的。
　　关键词：SBR；滗水器；水力学模型
　　中图分类号：X703.3
　　文献标识码：C
　　文章编号：1000-4602(2002)10-0064-04

　　滗水器是SBR工艺的关键设备，为适应其序批式处理的要求，滗水器必须在规定的时间内完成对反应器内澄清水的自流排放。因此，在设计选型时对滗水器进行排水量计算十分重要。

1　新型滗水器介绍

　　该滗水器从功能上可分为两部分，一是浮筒自平衡系统，其作用是实现滗水口高度随液位变化的自动调节；二是摆动堰管系统，其作用是防止进水和曝气时产生的悬浮污泥进入排水管。
　　①浮筒自平衡系统
　　由浮筒、排水支管、排水总管及回转轴管等部件组成。回转轴管是一兼具旋转和通导流体作用的复合机构。排水总管两端各与一个回转轴管相连，所以排水总管可以自由转动，排水支管通过铰接连杆与浮筒相连。当浮筒随液面升降而上下浮动时，堰管上的滗水口也随之同步移动，所以无论液面在什么位置，滗水口总是位于液面下，且与液面的距离基本保持不变，该距离的大小可以通过调整堰管的旋转角度加以调节。
　　②摆动堰管系统
　　包括堰管、回转轴管、减速电机、同步带和带轮、限位开关等部件。堰管两端各与一个回转轴管相连，所以堰管可以自由转动，堰管上径向伸出一段扁平的矩形管口，即滗水口。排水时流体从滗水口进入堰管，再经排水支管、排水总管流出。堰管的一侧装有同步带轮，减速电机通过同步带驱动堰管转动，从而带动堰管上的滗水口上下摆动(被抬高或者降低)。在需要阻渣的时候将滗水口抬离液面，而在需要排水的时候则将滗水口浸入液面。浮筒上的两个限位开关可以控制电机的启停和正反转。
　　该滗水器具有如下特点：
　　①阻渣效果可靠。在曝气、进水过程中滗水口可完全离开液面，因而彻底切断了浮渣进入排水管的途径；
　　②流动损失小。由于没有阀片等流阻较大的部件，流动通道中的损失仅为沿程损失和弯头及三通的损失，而流动阻力的减小可大大提高相同口径管道的自流排水量；
　　③驱动机构仅需使堰管上下摆动即可，因此电机功率较低、控制简单；
　　④结构简单，易于制造。

2　排水过程的水力学模型

　　在建立水力学模型前先做如下基本假定：
　　①水池或容器与排水管径相比足够大，排水过程可以按稳定流处理；
　　②考虑管道内的局部损失和沿程损失，并假定他们的计算满足叠加原则；
　　③水池或容器的水平截面积为常量，不随高度变化。
　　滗水器在自流状态下的排水过程可简化为如图1所示的形式，点1为滗水口，液体流速为V₁，点3为排水出口，管径为D₃，流速为V₃。点1至点3包括了滗水器的管道、弯头、三通、阀门等所有管件。设各段管道的管径、长度和流速分别为Di、Li和Vi，沿程损失系数为fi，弯头、三通和阀门的局部损失系数为Ki。容器的水平截面积为AR，液位(以点3为零点算起的高度)用y来表示。假设在排水过程中，液位从yA降到yB所需的时间为T，排出的累积流量为∑Q。

　　在排水时，设液面高度为y时的瞬时流量为Q，经过微元时间δt后液面下降了δy，则有：
?　　　　　　　Q·δt=-AR·δy
　　对上式从yA到yB进行积分，可得液面从A点降到B点的时间为：

　　因为水池与排水管径相比足够大，故液面降低很慢，可按稳定流状态应用伯诺里方程。从自由液面1点到排水口3点应用伯诺里方程：

　　　　　　　（V₁²／2g）+（P1／γ）+Z1=（V₃²／2g）+（P₃／γ）+Z3+∑hf+∑h_e　　(2)
　　总沿程损失∑hf=∑(fi·Li／Di·V_i²／2g)， 由连续性方程得V_i²·Di=V₃²·D₃，故总沿程损失可写为：
?　　　　　　∑hf=∑(fi·Li·D₃Di²)·V23/2g?(3)
　　若忽略局部损失之间的相互影响，由叠加原理得总局部损失为：
　　　　　　　∑he=∑Ki·V₃²／2g　　　　　(4)
　　式中∑K_i为管道各处的局部损失折算到出口流速V3时的损失系数之和。
　　又?　　　Q=（π／4）D₃²·V₃　　(5)
　　将式(1)、(2)、(3)、(4)、(5)联立，考虑到V1=0，P1=P3，y=Z1-Z3，则有：

　　　　V₃=｛(2g·y／［1+∑(fi·L_i·D₃／D_i²)+∑Ki］｝^0.5　　(6)
　　瞬时流量为：?
?　　　Q=｛(π/4)(D₃²·V₃=(π/4)D₃²·[2g·y/[1+∑(f_i·L_i·D₃D_i²)+∑Ki]｝^0.5 (7)
　　将式(7)代入式(1)，积分后可得液位从yA降到yB所需的时间为：

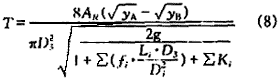
　　因为∑Q=AR(yA-yB)，故从式(8)中求出yB就可得到从液位高度yA开始排水t秒后的累积流量：

3　计算实例

　　滗水器(试验样机)的排水管径为50mm，图2为样机排水管路图，其简化图见图3。

　　从滗水器入口点1至出口点7处的损失有：矩形管口(点1)、三通(分支点2)、弯头(点3、3′) 、弯头(点4，4′)、三通(汇合点5)、阀门(点6)、弯头(点7)等处的局部水头损失(损失系数分别为K1、K₂、K₃、K₄、K₅、K₆、K₇)和2-3 -4-5、2-3′-4′-5′、5-7等直线管段的沿程损失(损失系数为f)。考虑到样机管路对称、管径不变的特点，则式(7)、(8)、(9)有如下结果：

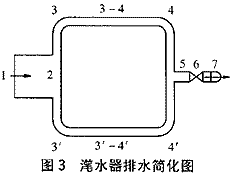
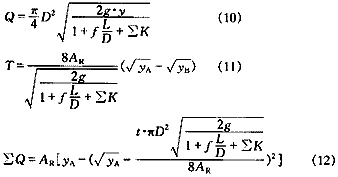
　　式中D——排水出口管径?
?　　　L——点2到点5直管段长度之和
?　　　∑K=K″1+K″₂+K₂₅+K₅+K₆+K₇　　　(13)?
　　其中K″₁=K₁·(A₅/A₁)²
?　　　　K″₂=K₂·(A₅/A₂)²
?　　　　K₂₅=1／4(D_5-6／D_2-5) ⁴·(K₃+fL_2-5／D_2-5+K₄)
　　式中D_2-5和D_5-6分别是2-5段和5-6段的管径，L_2-5是2-5直管段的长度。
　　试验用水槽的水平截面积(AR)为3.75m²，液位的初始高度为1.63m，结束高度为0.53m，即yA=1.63m，yB=0.53m。根据文献［1］、［2］和［3］提供的阻力损失系数的数据可以得出滗水器的Q、T和∑Q的表达式：
?　　　　Q=15.786(y)^0.5
?　　　　T=(7.5×3 600/15.786)[(y_A)^0.5-(y_B)^0.5 )?
　　　　　∑Q=3.75［yA-［(yA）^0.5-(15.786t/7.5×3600)²］?
　　表1是样机的实测数据和理论计算的比较，其中实测值为5次测量的算术平均值，理论值为按照上述公式得出的计算值。

表1　实测数据和理论计算的比较 高度(m) 瞬时流量Q(m³/h) 累积流量∑Q(m³) 排水时间T(s) 实测值 理论值 实测值 理论值 实测值 理论值 1.63 19.99 20.15 0 0 0 0 1.58 19.69 19.84 0.19 0.19 34.8 33.8 1.53 19.38 19.57 0.39 0.69 69.8 68.0 1.48 19.03 19.20 0.58 0.58 105.8 102.9 1.43 18.76 18.88 0.78 0.77 141.8 138.4 1.38 18.42 18.55 0.97 0.96 178.6 174.4 1.33 18.06 18.21 1.17 1.15 216.2 211.2 1.28 17.71 17.86 1.37 1.34 254.6 248.6 1.23 17.36 17.51 1.56 1.53 293.6 286.8 1.18 17.05 17.15 1.76 1.73 333.8 325.7 1.13 16.67 16.78 1.95 1.91 373.8 365.5 1.08 16.30 16.45 2.14 2.10 415.2 406.2 1.03 15.93 16.02 2.34 2.30 458.2 447.8 0.98 15.55 15.63 2.83 2.49 501.4 490.5 0.93 15.13 15.22 2.73 2.68 546.0 534.2 0.88 14.73 14.81 2.92 2.86 591.2 579.2 0.83 14.27 14.38 3.12 3.05 638.4 625.4 0.78 13.87 13.94 3.31 3.24 686.6 673.1 0.73 13.41 13.49 3.50 3.43 735.8 722.3 0.68 12.96 13.02 3.70 3.62 788.0 773.3 0.63 12.50 12.53 3.89 3.80 841.0 826.1 0.58 12.04 12.02 4.09 3.99 897.0 881.1 0.53 11.51 11.49 4.28 4.18 954.6 938.5

　　由表1可知，计算值与实测值的误差＜2%，这说明计算公式是正确的，可以在工程设计中使用。
　　自流状态下的排水流量是滗水器的主要性能指标，对于管径相同的滗水器，排水量大则经济性高。因此，滗水器的设计开发应追求用尽可能小的管径实现尽可能大的排水量，对于流量＞1000m³/h的大型滗水器更是如此。从式(10)可以看出，增大管径和减小流动损失系数都可以增大瞬时流量；从式(11)也可发现，在容器横截面不变且液位高度一定时，要想缩短排水时间，可通过增大排水管径和减小管系流动损失系数来实现；而当管径及水头损失一定时，在(yA-yB)不变即累积流量不变的条件下，使(yA-yB)值减小也可缩短排水时间。一般来说当其他条件一定时，减小滗水器内部管系及整个排水管路的流动损失是工程设计中需要着重考虑的问题。

4　结语

　　①该滗水器具有阻渣效果可靠、流动损失小、电机功率较低、控制简单等优点，值得大力推广。
　　②在考虑管道阻力损失的条件下得出的滗水器排水的瞬时流量、排水时间随排水液位高度变化的计算公式以及累积流量随排水时间的计算公式是正确的，为滗水器的设计和选型提供了理论依据。

参考文献：

　　［1］白铭声,王维新,陈祖苏.流体力学及流体机械［M］.北京：煤炭工业出版社，1980.
　　［2］Strecter V L,Wylie E B.周均长译.流体力学［M］.北京：高等教育出版社，1987.
　　［3］A·M·库尔干诺夫，H·Ф·菲得洛夫.郭连起译.给水排水系统水力计算手册［M］.北京：中国建筑工业出版社，1983.

　　电　　话：(021)58856638×2678(O)58951507(H)
　　E-mail:gujf@163.com
　　收稿日期：2002-04-28