利用BP网络建立预测城市用水量模型
单金林,戴雄奇,李江涛
(天津大学环境工程系,天津300072)
摘 要:利用神经网络法对城市用水量建立了具有时间序列的预测模型,并提出了基于该模型的数据处理方法,并结合某城市给水系统进行了用水量负荷预测,预测结果和实际情况有很好的一致性。
关键词:神经网络;预测;城市用水量
中图分类号:TU991.31
文献标识码:C
文章编号:1000-4602(2001)08-0061-03
用水量预测在城市建设规划、供水系统的调度管理中都具有重要作用。常用的预测方法可分为两类,一类是解释性预测方法,即找出被预测量的各影响因素,建立回归分析模型;另一类为时间序列分析方法,它只依赖于被预测量的历史观测数据及数据模式,通过序列分析,找出其顺序变化规律。因为城市用水量变化存在大量的不确定性因素,要找出系统内部的变化机理及各类因素之间相互影响的明确关系是比较困难的[1],这使得回归预测分析方法在用水量预测过程中的应用受到限制,而按时间顺序将观测或记录到的一组数据排列起来的时间序列分析方法,对外部影响因素复杂的作用进行简化,只考察历史观测数据及其数据模式随时间的内在变化规律,进而对整个系统进行描述和解释,以对系统未来状态作出预测。它比较符合用水量序列的特点,因而在用水量预测工作中应用较为广泛。但是对于不易建立精确数学模型、具有多种不确定性和非线性的系统,应用人工神经网络(ANN)和模糊逻辑系统(FLS)等智能预测方法往往可以处理传统方法难以解决的问题[2],而且人工神经网络不仅具有强大的映射能力,可以实现任何复杂的因果关系,而且还具有许多优秀品质,如:自适应、自训练和容错性等,能够从大量的历史数据中进行训练,进而找出某些行为变化的规律。
1 BP神经网络模型
神经网络模型中应用最为广泛的是BP网络模型,用其对城市供水系统的用水量进行预测,可取得良好的效果。BP网络即误差反向传递神经网络,这种网络不仅有输入输出层,而且有一层或多层隐含神经元,对输入的信息向前传递到隐层的神经元上,经过各神经元特性为Sigmoid型作用函数运算后,把隐层神经元的输出信息传递到输出神经元,最后给出结果。
该网络的训练过程由正向和反向传递两部分组成。在正向传递过程中,每一层神经元的状态只影响下一层神经元网络。如果输出层实际输出与期望输出值之间有误差,那么转入反向传递过程,将误差信号沿原来连接通路返回,通过修改各层神经元的权值,逐次向输入层传递进行计算,再经过正向传递过程,这两个过程反复运用,使误差信号满足实际要求[3]。
2 基于BP网络的用水量预测方法
对于城市用水量的时间序列而言,若已知前n天的用水量X(t)(t=1,2,…,n)。要预测第(n+1)天的用水量X(n+1)的值,首先需要构造BP网络的结构形式,即确定网络的输入输出模式。
①输入输出节点数的确定和训练样本的选取输入输出节点数是根据预测的实际需要确定,例如若预测某一时刻的用水量,输入节点数可取五个(即年、月、日、小时和星期),输出节点数取一个(即用水量);也可以输入节点数取一个(即日用水量),输出节点数也取一个(即日用水量)。若利用前一天24 h的时用水量来预
测后一天24 h的时用水量,输入输出节点数都取24个。对于训练样本的选取一般可采用以下方法:
将已知数据进行筛选作为样本数据,并将样本数据分成两部分,前者作为训练部分,后者作为检验部分。
②隐层层数和层内节点数的确定
隐层在BP网络内起抽象作用,即它能从输入中提取特征,增加隐层层数可增加人工神经网络的处理能力,但必将使训练复杂化,使训练时间增加。一般来说,开始设定一个隐层,然后按需要增加隐层数。
基于BP算法的神经网络中各层节点数的选取对网络的性能影响很大,它由网络的用途决定,但并不唯一,可用下面公式确定:设有m个输入节点数,n个输出节点数,则对于三层网络,隐层节点数为:mn(1)
对于四层网络,第一隐层节点数为:mR2(其中R=(n/m)1/3 (2)
第二隐层节点数为:mR (3)
3 程序流程图
神经网络的实施过程包括初始化、形成网络结构、对网络进行训练等操作,具体程序描述见图1、2。
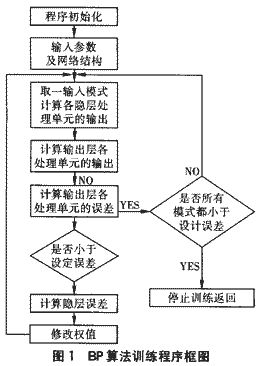
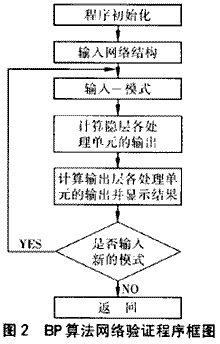
4 实例研究
已知某市连续8 d 24 h的时用水量,用Xi表示第i天24 h的时用水量。
若要求根据第8 d 24 h的时用水量来预测第9 d 24 h的时用水量,则需先对数据进行处理:
用前7 d的数据X1,X2,…,X7作为输入样本,后7 d的数据X2,X3,…,X8作为检验样本,对上面建好的网络进行训练,然后用X8作为输入,输出结果即为第9 d的时用水量。表1是预测值与实际值的比较。
(m3/h) 预测值
(m3/h) 相对误差
(%) 实际值
(m3/h) 预测值
(m3/h) 相对误差
(%) 11379 12327 -8.328 9 44816 45620 -1.7946 9380 9975 -6.345 9 60446 30142 0.9993 10744 11129 -3.585 7 18826 19437 -3.2468 14602 15170 -3.891 6 17873 18716 -4.7166 14849 14794 0.368 7 34764 35491 -2.0920 17891 17906 -0.085 2 70343 73337 -4.2566 24071 23679 1.627 5 79609 82914 -4.1519 24432 25497 -4.360 1 55931 56248 -0.5659 25747 25278 1.822 5 36386 34792 4.3822 25660 25232 1.668 9 31012 30938 0.2378 32061 32228 -0.521 7 19007 18492 2.7108 47073 44942 4.526 5 11278 11111 1.4785
由以上结果可以看出,在24个预测值中,只有2个预测值的相对误差值>5%,其他预测值误差均<5%,有的预测值与实际值相当接近,此预测结果令人满意。若作仿真曲线,两条曲线几乎重合,说明用BP网络预测城市用水量是可行的。使用此方法避免了计算各种参数,这为实际工作提供了便利的条件。
5 结论
①运用BP人工神经网络建立的城市用水量预测模型,在训练样本数据较好的情况下,具有较高的精度和可靠性。
②运用该方法通过系统输入输出数据即可建立较为准确的模型,模型的通用性和时效性只取决于样本数据的广泛及准确。
③运用该方法建立的预测模型可对不同时间作出准确的预测,为调度人员提供运行参数。
④值得注意的是,用该方法建立的模型若遇网络结构复杂,输入、输出节点较多时,运行时间则相对较长,大约需15~30 min。
⑤该方法只适用于递推式的预测问题。
参考文献:
[1]彭其定.城市用水量预测[J].中国给水排水,1989,5(5):59-62.
[2]蒋洪江,傅国伟.需水量的灰色预测[J].中国环境科学,1990,10(5):339-342.
[3]周继成.人工神经网络[M].北京:科学普及出版社,1993.
电 话:(022)27400830
E-mail:cygnetljt@eyou.com
收稿日期:2001-01-12
论文搜索
月热点论文
论文投稿
很多时候您的文章总是无缘变成铅字。研究做到关键时,试验有了起色时,是不是想和同行探讨一下,工作中有了心得,您是不是很想与人分享,那么不要只是默默工作了,写下来吧!投稿时,请以附件形式发至 paper@h2o-china.com ,请注明论文投稿。一旦采用,我们会为您增加100枚金币。








